《2025年名校题库八年级数学上册北师大版》

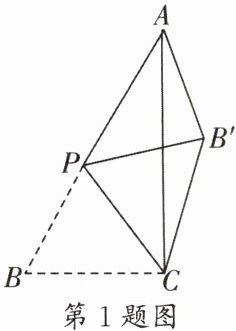
1. (锦江区期末)如图,在$\triangle ABC$中,$∠ACB = 90^{\circ}$,$AB = \sqrt{5}$,$BC = 1$,$P是线段AB$边上的动点(不与点$A$,$B$重合),将$\triangle BCP沿CP$所在直线翻折,得到$\triangle B'CP$,连接$B'A$,当$B'A$的长度取最小值时,$AP$的长度为______。

答案：
$\frac{2\sqrt{5}}{3}$ [解析]在$\triangle ABC$中，$\because \angle ACB = 90^{\circ}$，$AB = \sqrt{5}$，$BC = 1$，$\therefore AC = \sqrt{AB^{2}-BC^{2}} = 2$。由翻转变换的性质知，$CB' = BC = 1$。$\because CB'$长度固定不变，$\therefore$当$AB' + CB'$有最小值时，$AB'$的长度有最小值。根据两点之间线段最短可知，$A$，$B'$，$C$三点在一条直线上时，$AB'$有最小值，此时$AB' = AC - B'C = 2 - 1 = 1$。如图，过点$P$作$PE \perp BC$于点$E$，$PF \perp AC$于点$F$。$\because$将$\triangle BPC$沿直线$CP$翻折，$\therefore \angle ACP = \angle BCP = 45^{\circ}$。$\because PF \perp AC$，$PE \perp BC$，$\angle ACP = \angle BCP = 45^{\circ}$，$\therefore PF = PE$，$\therefore$四边形$PECF$是正方形，$\therefore PF = PE = CE = CF$。$\because S_{\triangle ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AC \cdot PF + \frac{1}{2}BC \cdot PE$，$\therefore 1 = \frac{3}{2}PF$，$\therefore PF = \frac{2}{3}$，$\therefore CF = PF = \frac{2}{3}$，$\therefore AF = AC - CF = 2 - \frac{2}{3} = \frac{4}{3}$。在$Rt\triangle APF$中，$AP = \sqrt{AF^{2}+PF^{2}} = \sqrt{(\frac{4}{3})^{2}+(\frac{2}{3})^{2}} = \frac{2\sqrt{5}}{3}$。

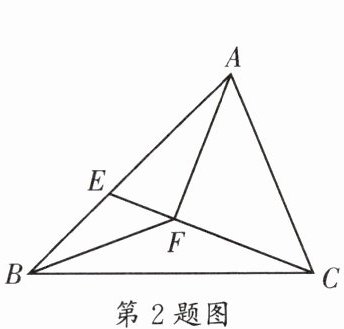
2. (青羊区期末)如图,在$\triangle ABC$中,$AB = CB$,$AC = 10$,$S_{\triangle ABC} = 60$,$E为AB$上一动点,连接$CE$,过点$A作AF⊥CE于点F$,连接$BF$,则$BF$的最小值是______。

7

答案： 解：取AC的中点O，连接OB，以AC为直径作圆。
∵AB=CB，AC=10，
∴OB⊥AC，AO=OC=5。
∵S_△ABC=60，
∴(1/2)×AC×OB=60，即(1/2)×10×OB=60，解得OB=12。
∵AF⊥CE，
∴点F在以AC为直径的圆上，OF=AO=5。
当点F在线段BO上时，BF最小，
∴BF=OB-OF=12-5=7。
答案：7

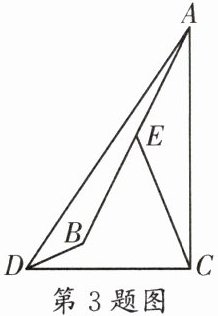
3. (树德实验)如图,在$Rt\triangle ADC$中,$CD⊥AC$,$AC = 8$,$DC = 6$,$AC绕点A摆动到AB$的位置,取$AB的中点E$,连接$BD$,$CE$,则$AC绕点A$摆动的过程中,$BD + CE$的最小值为______。

答案：
$2\sqrt{13}$ [解析]如图，取$AC$的中点$F$，连接$BF$，$DF$，$\therefore AF = \frac{1}{2}AC$。$\because E$是$AB$的中点，$\therefore AE = CF = \frac{1}{2}AB = \frac{1}{2}×8 = 4$。$\because AC = AB$，$\therefore AF = AE$。$\because \angle CAE = \angle BAF$，$\therefore \triangle CAE \cong \triangle BAF(SAS)$，$\therefore CE = BF$，$\therefore BD + CE = BD + BF$，$\therefore$当$D$，$B$，$F$三点共线时，$BD + CE$有最小值，最小值为$DF$。$\because BD + BF \geq FD$，$\therefore BD + CE \geq DF$。$\because CD \perp AC$，$\therefore \angle DCF = 90^{\circ}$，$\therefore DF = \sqrt{CF^{2}+CD^{2}} = \sqrt{4^{2}+6^{2}} = 2\sqrt{13}$，$\therefore BD + CE \geq 2\sqrt{13}$，$\therefore BD + CE$的最小值为$2\sqrt{13}$。

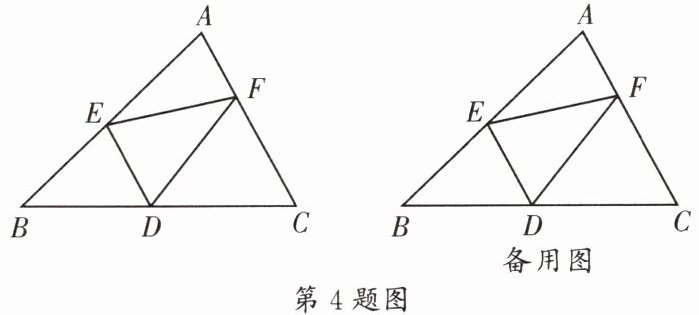
4. (树德实验)如图,在$\triangle ABC$中,$∠BAC = 75^{\circ}$,$∠ACB = 60^{\circ}$,$AC = 4$,则$\triangle ABC$的面积为______；$D$,$E$,$F分别为BC$,$AB$,$AC$上的动点,连接$DE$,$EF$,$FD$,则$\triangle DEF$的周长的最小值为______。

答案：
$6 + 2\sqrt{3}$ $3\sqrt{2} + \sqrt{6}$ [解析]如图1，过点$A$作$AH \perp BC$于点$H$。$\because \angle BAC = 75^{\circ}$，$\angle C = 60^{\circ}$，$\therefore \angle B = 180^{\circ} - \angle BAC - \angle C = 45^{\circ}$。又$\because AC = 4$，$\therefore$易得$CH = 2$，$AH = 2\sqrt{3}$。$\because \angle B = \angle BAH = 45^{\circ}$，$\therefore AH = BH = 2\sqrt{3}$，$\therefore BC = BH + CH = 2\sqrt{3} + 2$，$\therefore S_{\triangle ABC} = \frac{1}{2} \cdot BC \cdot AH = \frac{1}{2}×(2\sqrt{3} + 2)×2\sqrt{3} = 6 + 2\sqrt{3}$。

如图2，过点$B$作$BJ \perp AC$于点$J$，作点$F$关于$AB$的对称点$M$，点$F$关于$BC$的对称点$N$，连接$BM$，$BN$，$BF$，$MN$，$MN$交$AB$于点$E'$，交$BC$于点$D'$，此时$\triangle FE'D'$的周长$= MN$的长。$\because BF = BM = BN$，$\angle ABM = \angle ABF$，$\angle CBF = \angle CBN$，$\therefore \angle MBN = 2\angle ABC = 90^{\circ}$，$\therefore \triangle BMN$是等腰直角三角形，$\therefore BM$的值最小时，$MN$的值最小。根据垂线段最短可知，当$BF$与$BJ$重合时，$BM$的值最小。$\because BJ = \frac{2S_{\triangle ABC}}{AC} = \frac{12 + 4\sqrt{3}}{4} = 3 + \sqrt{3}$，$\therefore MN$的最小值为$\sqrt{2}BJ = \sqrt{2}×(3 + \sqrt{3}) = 3\sqrt{2} + \sqrt{6}$，$\therefore \triangle DEF$的周长的最小值为$3\sqrt{2} + \sqrt{6}$。

5. (天府新区期末)如图,在$\triangle ABC$中,$∠ACB = 90^{\circ}$,$BC = 3$,$AC = 4$,$E为线段BC$上一动点(点$E不与点B$,$C$重合),$F为线段AC$上一动点(点$F不与点A$,$C$重合),且始终满足$BE = CF$,连接$AE$,$BF$,则$AE + BF$的最小值为______。

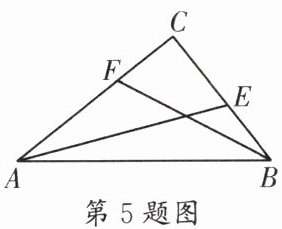
答案：
$\sqrt{58}$ [解析]如图，在$AC$上截取$CD = BC = 3$，过点$D$作$DM \perp DC$，且使$DM = AC = 4$，连接$MF$。$\because CF = BE$，$\therefore DF = CE$。又$\because \angle ACE = \angle MDF = 90^{\circ}$，$\therefore \triangle MDF \cong \triangle ACE(SAS)$，$\therefore MF = AE$，$\therefore AE + BF = MF + BF$。当$M$，$F$，$B$三点共线时，$AE + BF$有最小值，最小值为$BM$。过点$B$作$BN \perp MD$，交$MD$的延长线于点$N$，则四边形$CDNB$是正方形，$\therefore DN = BC = CD = BN = 3$，$\therefore MN = DM + DN = 7$，$\therefore BM = \sqrt{BN^{2}+MN^{2}} = \sqrt{3^{2}+7^{2}} = \sqrt{58}$，$\therefore AE + BF$的最小值为$\sqrt{58}$。

6. (金牛区期末)如图,在$Rt\triangle ABC$中,$∠ACB = 90^{\circ}$,$∠ABC = 30^{\circ}$,$AC = 4$,$D为斜边AB$上一点,且$∠ADC = 45^{\circ}$,以$CD$为边、点$D为直角顶点作Rt\triangle CDP$,$M为CP$的中点,连接$MB$,则$MB$长度的最小值为______。

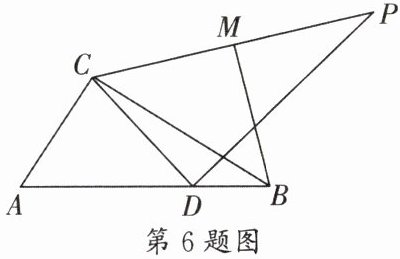
答案：
$3\sqrt{2}$ [解析]如图，过点$C$作$CN \perp AB$于点$N$，作$CD$的垂直平分线$l$。$\because \angle CDA = 45^{\circ}$，$CN \perp AB$，$\therefore l$经过点$N$。$\because M$是$Rt\triangle CDP$的斜边的中点，$\therefore$点$M$到点$C$的距离等于点$M$到点$D$的距离，$\therefore$点$M$在直线$l$上。过点$B$作$BM' \perp l$于点$M'$，$\therefore$当点$M$与点$M'$重合时$MB$最短。$\because AC = 4$，$\angle ABC = 30^{\circ}$，$\angle ACB = 90^{\circ}$，$\therefore \angle A = 60^{\circ}$，$AB = 8$，$\therefore \angle ACN = 30^{\circ}$，$BC = \sqrt{8^{2}-4^{2}} = 4\sqrt{3}$，$\therefore AN = 2$，$\therefore BN = 8 - 2 = 6$。由已知易得$CD // BM'$，$\therefore \angle M'BD = \angle CDN = 45^{\circ}$，$\therefore BM' = \frac{6}{\sqrt{2}} = 3\sqrt{2}$，故$MB$长度的最小值为$3\sqrt{2}$。