《2025年名校题库八年级数学上册北师大版》

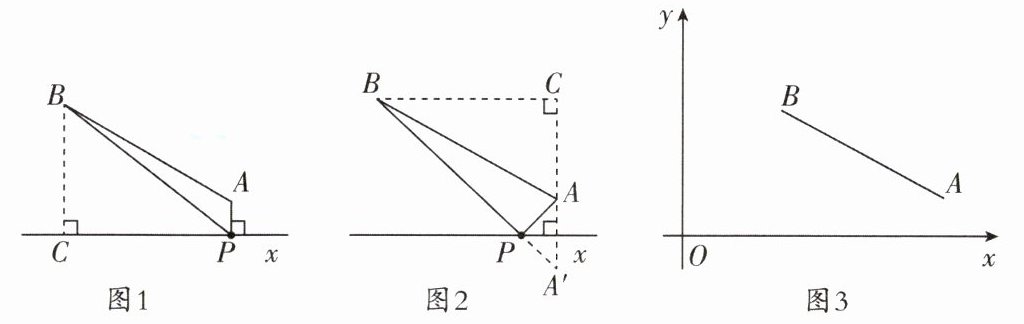
4. (嘉祥)恩施州自然风光无限,特别是以“雄、奇、秀、幽、险”著称于世. 著名的恩施大峡谷(用字母$A$表示)和世界级自然保护区星斗山(用字母$B$表示)位于笔直的沪渝高速公路$x$的同侧,$AB = 50\mathrm{km}$,$A$,$B到直线x$的距离分别为 10 km 和 40 km,要在沪渝高速公路旁修建一服务区$P$,向$A$,$B$两景区运送游客. 小明设计了两种方案:图 1 是方案一的示意图($AP与直线x$垂直,垂足为$P$),点$P到点A$,$B的距离之和S_{1} = PA + PB$;图 2 是方案二的示意图(点$A关于直线x的对称点是A'$,连接$BA'交直线x于点P$),点$P到点A$,$B的距离之和S_{2} = PA + PB$.
(1)求$S_{1}$,$S_{2}$,并比较它们的大小;
(2)请你说明$S_{2} = PA + PB$的值为最小;
(3)拟建的恩施州到张家界的高速公路$y$与沪渝高速公路垂直,建立如图 3 所示的平面直角坐标系,点$B到直线y$的距离为 30 km,请你在$x旁和y旁各修建一服务区P$,$Q$,使点$P$,$A$,$B$,$Q$组成的四边形的周长最小,并求出这个最小值.

答案：
解：
(1)如图 1，过点 $A$ 作 $AD\perp BC$ 交 $BC$ 于点 $D$，$\therefore CD=AP=10km$。$\because BC=40km$，$\therefore BD=30km$。$\because AB=50km$，$\therefore AD=40km$，$\therefore PC=40km$，$\therefore BP=40\sqrt {2}km$，$\therefore S_{1}=PA+PB=(10+40\sqrt {2})km$。如图 2，$\because BC=40km$，$A'C=50km$，$\therefore S_{2}=PA+PB=PA'+PB=A'B=\sqrt {40^{2}+50^{2}}=10\sqrt {41}(km)$，$\therefore S_{1}＞S_{2}$。

(2)如图 2，在公路上任找一点 $M$，连接 $MA$，$MB$，$MA'$。由轴对称，知 $MA=MA'$，$\therefore MB+MA=MB+MA'\geqslant A'B$，$\therefore S_{2}=BA'=PA+PB$ 最小。
(3)如图 3，作点 $A$ 关于 $x$ 轴的对称点 $A'$，作点 $B$ 关于 $y$ 轴的对称点 $B'$，连接 $A'B'$ 交 $x$ 轴于点 $P$，交 $y$ 轴于点 $Q$，则点 $P$，$Q$ 即为所求。过点 $A'$，$B'$ 分别作 $x$ 轴和 $y$ 轴的平行线交于点 $G$，$\therefore A'G=100km$，$B'G=50km$，$\therefore A'B'=50\sqrt {5}km$，$\therefore$ 四边形 $ABQP$ 周长最小为 $(50+50\sqrt {5})km$。