第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
1. (高新区期末)为了增强居民的节水意识,从2017年1月1日起,成都城区水价执行“阶梯式”计费,每月应交水费$y$(元)与用水量$x$(吨)之间的函数关系如图所示。若某用户5月份交水费18.05元,则该用户该月用水
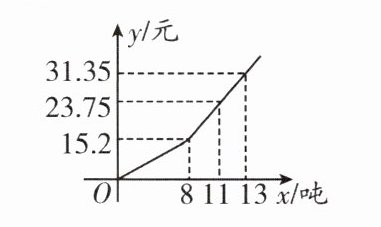
9
吨。
答案:
解:设当 $ x \geq 8 $ 时,$ y = kx + b $。
将点 $ (8,15.2) $,$ (11,23.75) $ 代入,得
$\begin{cases} 8k + b = 15.2 \\ 11k + b = 23.75 \end{cases}$
解得 $\begin{cases} k = 2.85 \\ b = -7.6 \end{cases}$
$\therefore y = 2.85x - 7.6$
由题意,得 $ 2.85x - 7.6 = 18.05 $
解得 $ x = 9 $
答:该用户该月用水 9 吨。
将点 $ (8,15.2) $,$ (11,23.75) $ 代入,得
$\begin{cases} 8k + b = 15.2 \\ 11k + b = 23.75 \end{cases}$
解得 $\begin{cases} k = 2.85 \\ b = -7.6 \end{cases}$
$\therefore y = 2.85x - 7.6$
由题意,得 $ 2.85x - 7.6 = 18.05 $
解得 $ x = 9 $
答:该用户该月用水 9 吨。
2. (武侯区期末)某市为了鼓励居民在枯水期(当年11月至第二年5月)节约用电,规定7:00至23:00为用电高峰期,此期间用电电费$y_{1}$(单位:元)与用电量$x$(单位:度)之间满足的关系如图所示;规定23:00至第二天早上7:00为用电低谷期,此期间用电电费$y_{2}$(单位:元)与用电量$x$(单位:度)之间满足如表所示的一次函数关系。
(1)求$y_{2}与x$之间的函数关系式,并直接写出当$0\leqslant x\leqslant 180和x>180$时,$y_{1}与x$之间的函数关系式;
(2)若市民王先生一家在12月份共用电350度,支付电费150元,求王先生一家在高峰期和低谷期各用电多少度。

(1)求$y_{2}与x$之间的函数关系式,并直接写出当$0\leqslant x\leqslant 180和x>180$时,$y_{1}与x$之间的函数关系式;
(2)若市民王先生一家在12月份共用电350度,支付电费150元,求王先生一家在高峰期和低谷期各用电多少度。
答案:
(1)设$y_{2}$与$x$之间的函数关系式为$y_{2}=k_{2}x + b_{2}$,根据题意,得$\left\{\begin{array}{l}80k_{2}+b_{2}=20\\100k_{2}+b_{2}=25\end{array}\right.$,解得$\left\{\begin{array}{l}k_{2}=0.25\\b_{2}=0\end{array}\right.$,$\therefore y_{2}=0.25x$。
当$0\leqslant x\leqslant180$时,$y_{1}=\frac{90}{180}x = 0.5x$。
当$x>180$时,设$y_{1}=k_{1}x + b_{1}$,根据题意,得$\left\{\begin{array}{l}180k_{1}+b_{1}=90\\280k_{1}+b_{1}=150\end{array}\right.$,解得$\left\{\begin{array}{l}k_{1}=0.6\\b_{1}=-18\end{array}\right.$,$\therefore y_{1}=0.6x - 18$。
综上,$y_{1}=\left\{\begin{array}{l}0.5x(0\leqslant x\leqslant180)\\0.6x - 18(x>180)\end{array}\right.$。
(2)设王先生一家在高峰期用电$x$度,低谷期用电$y$度。
当$0\leqslant x\leqslant180$时,$\left\{\begin{array}{l}x + y=350\\0.5x + 0.25y=150\end{array}\right.$,解得$\left\{\begin{array}{l}x=250\\y=100\end{array}\right.$(不合题意,舍去)。
当$x>180$时,$\left\{\begin{array}{l}x + y=350\\0.6x - 18 + 0.25y=150\end{array}\right.$,解得$\left\{\begin{array}{l}x=230\\y=120\end{array}\right.$。
答:王先生一家在高峰期用电230度,低谷期用电120度。
(1)设$y_{2}$与$x$之间的函数关系式为$y_{2}=k_{2}x + b_{2}$,根据题意,得$\left\{\begin{array}{l}80k_{2}+b_{2}=20\\100k_{2}+b_{2}=25\end{array}\right.$,解得$\left\{\begin{array}{l}k_{2}=0.25\\b_{2}=0\end{array}\right.$,$\therefore y_{2}=0.25x$。
当$0\leqslant x\leqslant180$时,$y_{1}=\frac{90}{180}x = 0.5x$。
当$x>180$时,设$y_{1}=k_{1}x + b_{1}$,根据题意,得$\left\{\begin{array}{l}180k_{1}+b_{1}=90\\280k_{1}+b_{1}=150\end{array}\right.$,解得$\left\{\begin{array}{l}k_{1}=0.6\\b_{1}=-18\end{array}\right.$,$\therefore y_{1}=0.6x - 18$。
综上,$y_{1}=\left\{\begin{array}{l}0.5x(0\leqslant x\leqslant180)\\0.6x - 18(x>180)\end{array}\right.$。
(2)设王先生一家在高峰期用电$x$度,低谷期用电$y$度。
当$0\leqslant x\leqslant180$时,$\left\{\begin{array}{l}x + y=350\\0.5x + 0.25y=150\end{array}\right.$,解得$\left\{\begin{array}{l}x=250\\y=100\end{array}\right.$(不合题意,舍去)。
当$x>180$时,$\left\{\begin{array}{l}x + y=350\\0.6x - 18 + 0.25y=150\end{array}\right.$,解得$\left\{\begin{array}{l}x=230\\y=120\end{array}\right.$。
答:王先生一家在高峰期用电230度,低谷期用电120度。
3. (成华区期末)某通讯公司就手机流量套餐推出$A$,$B$,$C$三种方案(如下表),三种方案每月所需的费用$y$(元)与每月使用的流量$x$(兆)之间的函数图象如图所示。
| |$A$方案|$B$方案|$C$方案|
|每月基本费用(元)|20|56|266|
|每月免费使用流量(兆)|1024|$m$|无限|
|超出后每兆收费(元)|$n$|$n$| |
结合表格和图象解答下列问题:
(1)填空:表中$m=$
(2)在$A$方案中,当每月使用的流量不少于1024兆时,求每月所需的费用$y$(元)与每月使用的流量$x$(兆)之间的函数关系式;
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择$C$方案最划算?
| |$A$方案|$B$方案|$C$方案|
|每月基本费用(元)|20|56|266|
|每月免费使用流量(兆)|1024|$m$|无限|
|超出后每兆收费(元)|$n$|$n$| |
结合表格和图象解答下列问题:
(1)填空:表中$m=$
3072
,$n=$0.3
;(2)在$A$方案中,当每月使用的流量不少于1024兆时,求每月所需的费用$y$(元)与每月使用的流量$x$(兆)之间的函数关系式;
设在A方案中,当每月使用的流量不少于1024兆时,函数关系式为$y = kx + b(k \neq 0)$。
把$(1024, 20)$,$(1144, 56)$代入,得$\begin{cases}1024k + b = 20 \\1144k + b = 56\end{cases}$,
解得$\begin{cases}k = 0.3 \\b = -287.2\end{cases}$,
$\therefore y = 0.3x - 287.2(x \geq 1024)$
把$(1024, 20)$,$(1144, 56)$代入,得$\begin{cases}1024k + b = 20 \\1144k + b = 56\end{cases}$,
解得$\begin{cases}k = 0.3 \\b = -287.2\end{cases}$,
$\therefore y = 0.3x - 287.2(x \geq 1024)$
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择$C$方案最划算?
在B方案中,当每月使用的流量不少于3072兆时,$y = 56 + 0.3(x - 3072)$。
令$56 + 0.3(x - 3072) = 266$,
解得$x = 3772$。
当每月使用的流量超过3772兆时,选择C方案最划算。
令$56 + 0.3(x - 3072) = 266$,
解得$x = 3772$。
当每月使用的流量超过3772兆时,选择C方案最划算。
答案:
(1)3072;0.3
(2)设在A方案中,当每月使用的流量不少于1024兆时,函数关系式为$y = kx + b(k \neq 0)$。
把$(1024, 20)$,$(1144, 56)$代入,得$\begin{cases}1024k + b = 20 \\1144k + b = 56\end{cases}$,
解得$\begin{cases}k = 0.3 \\b = -287.2\end{cases}$,
$\therefore y = 0.3x - 287.2(x \geq 1024)$
(3)在B方案中,当每月使用的流量不少于3072兆时,$y = 56 + 0.3(x - 3072)$。
令$56 + 0.3(x - 3072) = 266$,
解得$x = 3772$。
当每月使用的流量超过3772兆时,选择C方案最划算。
(1)3072;0.3
(2)设在A方案中,当每月使用的流量不少于1024兆时,函数关系式为$y = kx + b(k \neq 0)$。
把$(1024, 20)$,$(1144, 56)$代入,得$\begin{cases}1024k + b = 20 \\1144k + b = 56\end{cases}$,
解得$\begin{cases}k = 0.3 \\b = -287.2\end{cases}$,
$\therefore y = 0.3x - 287.2(x \geq 1024)$
(3)在B方案中,当每月使用的流量不少于3072兆时,$y = 56 + 0.3(x - 3072)$。
令$56 + 0.3(x - 3072) = 266$,
解得$x = 3772$。
当每月使用的流量超过3772兆时,选择C方案最划算。
查看更多完整答案,请扫码查看


