《2025年名校题库八年级数学上册北师大版》

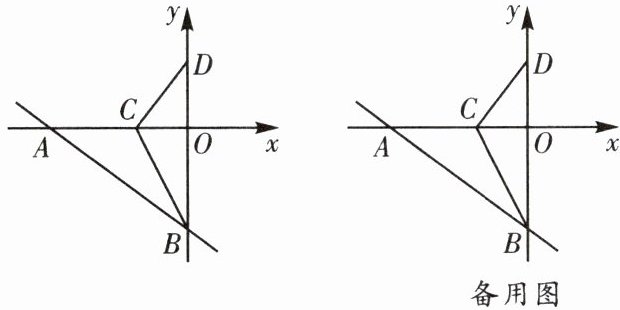
5. (锦江区期末)如图,直线$y= kx+b与x$轴、$y轴分别交于点A和点B$,点$C在线段AO$上,将$\triangle ABC沿BC$所在直线折叠后,点$A恰好落在y轴上的点D$处。若$OA= 4$,$OD= 2$。
(1)求直线$AB$的表达式。
(2)求$S_{\triangle ABC}:S_{\triangle COD}$的值。
(3)在直线$CD上是否存在点P$,使得$∠PBC= 45^{\circ }$？若存在,请直接写出点$P$的坐标。

答案：
5.解:
(1)由题知BD=BA.设OB=m,则BD=m+2.在Rt△OAB中,OA²+OB²=AB²,即4²+m²=
(m+2)²,
∴m=3,
∴B(O,-3).
又
∵A(-4,0),
∴直线AB的表达式为y=
-$\frac{3}{4}$x-3.
(2)设OC=a,则AC=4-a.
由折叠的性质,知CD=CA=4-a.
在Rt△OCD中,OC²+OD²=CD²,
∴a²+2²=
(4-a)²,
∴a=$\frac{3}{2}$,
∴AC=OA−OC=$\frac{5}{2}$,
∴SABC=$\frac{1}{2}$AC.OB=$\frac{1}{2}$×$\frac{5}{2}$×3=$\frac{15}{4}$,S△OD=
$\frac{1}{2}$OC.OD=$\frac{1}{2}$×$\frac{3}{2}$×2=$\frac{3}{2}$,
∴SABC.SOD=$\frac{15}{4}$:$\frac{3}{2}$=$\frac{5}{2}$.
(3)存在.如图1,当点P在第三象限内时,过点C作CM⊥PB于点M,过点M作NE⊥x轴于点E,MF⊥y轴于点F,则CM=MB,∠MEC=
∠MFB=90°,
又
∵∠EMF=∠CMB=90°,
∴∠EMC=
∠FMB,
∴△MCE≌△MBF(AAS),
∴ME=
MF,CE=BF;
又
∵ME⊥x轴,MF⊥y轴,
∴四边形EMFO为正方形,
$\frac{3}{2}$+3
∴OE=OF=$\frac{OC+OB}{2}$=2=$\frac{9}{4}$,
∴M(-$\frac{9}{4}$,-$\frac{9}{4}$),
∴直线BM的表达式为y=-$\frac{1}{3}$x-3.
∵c(-$\frac{3}{2}$,0)),D(0,,2),
∴直线CD的表达式为y=$\frac{4}{3}$x+2.
y=-$\frac{1}{3}$x-3,
联立x+2,解得{xy==−−32,,
∴P(−3,−2)).
y=$\frac{4}{3}$
如图2,当点P在第一象限内时,过点C作CM⊥PB于点M,过点M作ME⊥x轴于点E,MF⊥y轴于点F,则CM=MB,∠MEC=∠MFB=90°.又
∵∠EMF=∠CMB=90°,
∴∠EMC=∠FMB,
∴△MCE≌△MBF(AAS),
∴ME=MF,CE=BF.
又
∵ME⊥x轴,MF⊥y轴，
∴四边形EMFO为正方形，
3−$\frac{3}{2}$
∴OE=OF=$\frac{OB−}{2}$=2=$\frac{3}{4}$,
∴M($\frac{3}{4}$,-$\frac{3}{4}$),
∴直线BM的表达式为y=3x-3.
联立{yy==$\frac{4}{3}$3x−x+3,2,解得{xy==36,,
∴P(3,6).
综上所述,点P的坐标为(−3,−2)或(3,6).