《2025年名校题库八年级数学上册北师大版》

4. (武侯区期末)如图,在平面直角坐标系$xOy$中,直线$l:y = - x + m与x轴交于点A$,点$B在x$轴的负半轴上,且$OB = \frac{1}{2}OA = 2$。
(1)求直线$l$的函数表达式。
(2)$P是直线l$上一点,连接$BP$,将线段$BP绕点B顺时针旋转90^{\circ}得到BQ$。
(ⅰ)当点$Q落在y$轴上时,连接$AQ$,求点$P的坐标及四边形APBQ$的面积；
(ⅱ)作直线$BP$,$AQ$,且两条直线在第一象限内相交于点$C$,记四边形$APBQ的面积为S_{1}$,$\triangle ABC的面积为S_{2}$,若$S_{2} = \frac{1}{3}S_{1}$,求点$Q$的坐标。

答案：
4.解:
(1)
∵$OB=\frac{1}{2}OA = 2$，
∴$OA = 4$，
∴$A(4,0)$.
∵直线$l:y = -x + m$与$x$轴交于点$A$，
∴$-4 + m = 0$，解得$m = 4$，
∴直线$l$的函数表达式为$y = -x + 4$.
(2)(i)如图1，设点$P(p,-p + 4)$，过点$P$作$PD\perp x$轴于点$D$.
　　　　　
∵$OB=\frac{1}{2}OA = 2$，$OA = 4$，
∴$AB = OA + OB = 6$.
∵$\angle BOQ=\angle PDB=\angle QBP = 90^{\circ}$，
∴$\angle BQO+\angle QBO = 90^{\circ}$，$\angle PBD+\angle QBO = 90^{\circ}$，
∴$\angle BQO=\angle PBD$，
又
∵$PB = BQ$，
∴$\triangle PDB\cong\triangle BOQ(AAS)$，
∴$PD = BO = 2=-p + 4$，$OQ = DB = 2 + p$，
∴$p = 2$，
∴点$P$的坐标为$(2,2)$，点$Q$的坐标为$(0,-4)$，
∴$S_{四边形APBQ}=S_{\triangle APB}+S_{\triangle AQB}=\frac{1}{2}×6×2+\frac{1}{2}×6×4 = 18$.
(ii)设点$P(n,-n + 4)$，如图2，过点$C$作$CF\perp x$轴于点$F$，过点$P$作$PG\perp x$轴于点$G$，过点$Q$作$QE\perp x$轴于点$E$.
　　　　　
与(i)同理可得$\triangle PGB\cong\triangle BEQ(AAS)$，
∴$PG = BE=-n + 4$，$EQ = GB = 2 + n$，
∴$OE = OB - BE = 2 + n - 4 = n - 2$，
∴$Q(-n + 2,-n - 2)$，
∴$S_{1}=\frac{1}{2}AB\cdot(-n + 4)+\frac{1}{2}AB\cdot(n + 2)=\frac{1}{2}×6×(-n + 4)+\frac{1}{2}×6×(n + 2)=18$，
∴$S_{2}=\frac{1}{3}S_{1}=\frac{1}{2}×6CF = 6$，
∴$CF = 2$.
设直线$AQ$的解析式为$y = kx + a$，
∴$\begin{cases}4k + a = 0\\(-n + 2)k + a = -n - 2\end{cases}$解得$\begin{cases}k = 1\\a = -4\end{cases}$
∴直线$AQ$的解析式为$y = x - 4$，
∴$C(6,2)$.
设直线$BC$的解析式为$y = sx + t$，
∴$\begin{cases}6s + t = 2\\-2s + t = 0\end{cases}$解得$\begin{cases}s=\frac{1}{4}\\t=\frac{1}{2}\end{cases}$
∴直线$BC$的解析式为$y=\frac{1}{4}x+\frac{1}{2}$.
　联立$\begin{cases}y = -x + 4\\y=\frac{1}{4}x+\frac{1}{2}\end{cases}$解得$\begin{cases}x=\frac{14}{5}\\y=\frac{6}{5}\end{cases}$
∴$P(\frac{14}{5},\frac{6}{5})$，
∴$n=\frac{14}{5}$，
∴点$Q$的坐标为$(-\frac{4}{5},-\frac{24}{5})$.

5. (高新区期末)如图1,已知直线$y = 2x + 2与y$轴、$x轴分别交于A$,$B$两点,以$B为直角顶点在第二象限作等腰Rt\triangle ABC$。
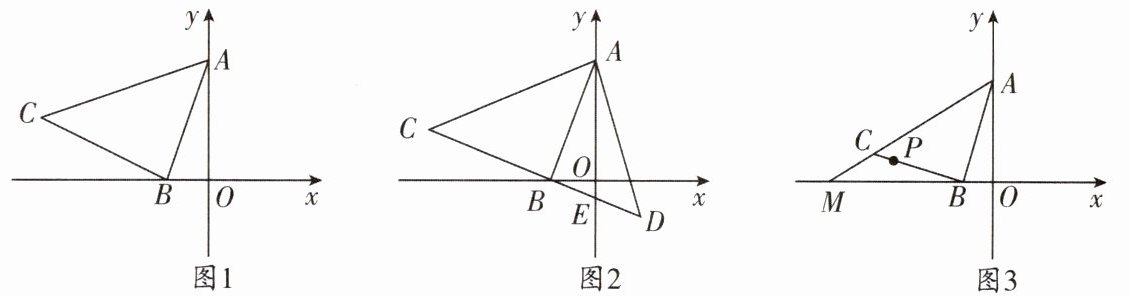
(1)求点$C$的坐标,并求出直线$AC$的表达式。
(2)如图2,直线$CB交y轴于点E$,在直线$CB上取一点D$,连接$AD$,若$AD = AC$,求证：$BE = DE$。
(3)如图3,在(1)的条件下,直线$AC交x轴于点M$,$P( - \frac{5}{2},k)是线段BC$上一点,在线段$BM上是否存在一点N$,使直线$PN平分\triangle BCM$的面积？若存在,请求出点$N$的坐标；若不存在,请说明理由。

答案：
5.
(1)解:由题知，点$A(0,2)$，$B(-1,0)$，
∴$OB = 1$，$OA = 2$.如图1，过点$C$作$CQ\perp x$轴于点$Q$.
∵$\angle OBA+\angle OAB = 90^{\circ}$，$\angle OBA+\angle QBC = 90^{\circ}$，
∴$\angle OAB=\angle QBC$；又
∵$AB = BC$，$\angle AOB=\angle BQC = 90^{\circ}$，
∴$\triangle ABO\cong\triangle BCQ$，
∴$BQ = AO = 2$，$CQ = OB = 1$，
∴$OQ = BQ + BO = 3$，
∴$C(-3,1)$.设直线$AC$的表达式为$y = ax + b$，则$\begin{cases}1 = -3a + b\\2 = b\end{cases}$解得$\begin{cases}a=\frac{1}{3}\\b = 2\end{cases}$
∴直线$AC$的表达式为$y=\frac{1}{3}x + 2$.
　　　　　
(2)证明:如图2，过点$C$作$CH\perp x$轴于点$H$，过点$D$作$DF\perp x$轴于点$F$，$DG\perp y$轴于点$G$.
∵$AC = AD$，$AB\perp CB$，
∴$BC = BD$.又
∵$\angle CBH=\angle DBF$，$\angle BHC=\angle BFD = 90^{\circ}$，
∴$\triangle BCH\cong\triangle BDF$，
∴$BF = BH = 2$，
∴$OF = OB = 1$，
∴$DG = OB$.又
∵$\angle BOE=\angle DGE$，$\angle BEO=\angle DEG$，
∴$\triangle BOE\cong\triangle DGE$，
∴$BE = DE$；
　　　　　
(3)解:如图3，由点$C(-3,1)$，$B(-1,0)$可得直线$BC:y=-\frac{1}{2}x-\frac{1}{2}$，将$P(-\frac{5}{2},k)$代入直线$BC$的解析式，得$k=\frac{3}{4}$，
∴$P(-\frac{5}{2},\frac{3}{4})$.由$y=\frac{1}{3}x + 2$，得点$M(-6,0)$，
∴$BM = 5$，则$S_{\triangle BCM}=\frac{5}{2}$.若存在点$N$，则$\frac{1}{2}BN\cdot\frac{3}{4}=\frac{1}{2}×\frac{5}{2}$，
∴$BN=\frac{10}{3}$，
∴$ON=\frac{13}{3}$.
∵$BN＜BM$，
∴$N(-\frac{13}{3},0)$.