《2025年名校题库八年级数学上册北师大版》

1. (武侯区期末)如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所爬行的最短路线的长是 (B)
A.$3\sqrt{2}+8$
B.10
C.14
D.无法确定

答案： 解：将长方体纸箱侧面展开，有两种情况：
情况1：展开前面和上面（或后面和下面），此时A、B两点间的水平距离为3+3=6，垂直距离为8，路线长为$\sqrt{6^2 + 8^2} = 10$；
情况2：展开前面和右面（或其他相邻侧面），此时A、B两点间的水平距离为3，垂直距离为8+3=11，路线长为$\sqrt{3^2 + 11^2} = \sqrt{130} ＞ 10$。
比较得最短路线长为10。
答案：B

2. (七中育才)有一长、宽、高分别为5cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱。请你算一算,能放入的细木条的最大长度是 (C)
A.$\sqrt{41}$cm
B.$\sqrt{34}$cm
C.$5\sqrt{2}$cm
D.$5\sqrt{3}$cm

答案： 解：长方体木箱的体对角线是能放入的最长木条。
体对角线长度公式为：$\sqrt{长^2 + 宽^2 + 高^2}$
代入长5cm、宽4cm、高3cm，得：
$\sqrt{5^2 + 4^2 + 3^2} = \sqrt{25 + 16 + 9} = \sqrt{50} = 5\sqrt{2}$cm
答案：C

3. (青羊区期末)如图,长方体的长为15,宽为10,高为20,点B到点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是 (B)
A.$5\sqrt{21}$
B.25
C.$10\sqrt{5}+5$
D.35

答案： 解：将长方体表面展开，蚂蚁爬行路径为平面上两点间线段，分两种情况：
情况1： 展开前面和上面（或后面和下面）
横向距离：$15 + (10 - 5) = 20$，纵向距离：20
最短距离：$\sqrt{20^2 + 20^2} = 20\sqrt{2} \approx 28.28$
情况2： 展开前面和右面（或左面和后面）
横向距离：$10 + 5 = 15$，纵向距离：20
最短距离：$\sqrt{15^2 + 20^2} = 25$
比较得最短距离为25。
答案：B

4. (成外)如图,有一个圆柱,它的高为13cm,底面周长为10cm,在圆柱的下底面上的A点处有一只蚂蚁,它想吃到离上底面1cm与A点相对的B点处的食物,需要爬行的最短距离为______。

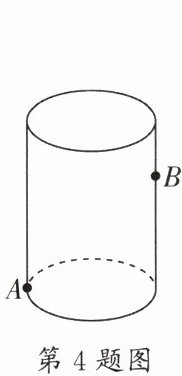
13 cm

答案： 解：将圆柱侧面沿过A点的母线展开，得到一个长方形。
长方形的长为圆柱底面周长的一半，即 $ \frac{10}{2} = 5 \, \text{cm} $；
长方形的宽为蚂蚁爬行的垂直高度，即圆柱高减去B点离上底面的距离： $ 13 - 1 = 12 \, \text{cm} $。
最短距离为展开后长方形的对角线长，由勾股定理得：
$ \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \, \text{cm} $。
13 cm

5. (嘉祥)如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为15cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,且位于离容器上沿3cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为21cm,则该容器底面的周长为______cm。

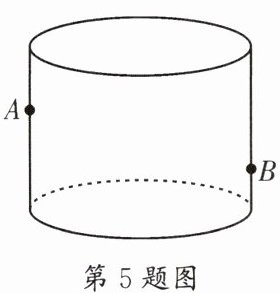
14√5

答案： 解：将圆柱侧面展开，设容器底面周长为 $ C $，则展开图矩形的长为 $ C $，宽为圆柱的高15cm。
作点A关于展开图上沿的对称点 $ A' $，则 $ A' $ 到上沿的距离也为3cm，所以 $ A' $ 到容器底部的距离为 $ 15 - 3 = 12 $ cm。点B离容器底部4cm，故在展开图中，$ A' $ 与B的竖直距离为 $ 12 + 4 = 16 $ cm。
蚂蚁爬行的最短路径为 $ A'B = 21 $ cm，根据勾股定理，$ A'B^2 = (\frac{C}{2})^2 + 16^2 $（因最短路径对应半个周长的水平距离）。
即 $ 21^2 = (\frac{C}{2})^2 + 16^2 $，解得 $ (\frac{C}{2})^2 = 441 - 256 = 185 $，$ \frac{C}{2} = \sqrt{185} $，$ C = 2\sqrt{185} = 14\sqrt{5} $。
答案：$ 14\sqrt{5} $

6. (西川)如图,在一个长方形草坪ABCD上放着一根长方体木块。已知AD= 6米,AB= 4米,该木块的较长边与AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A爬过木块到达点C处需要爬的最短路程是______米。

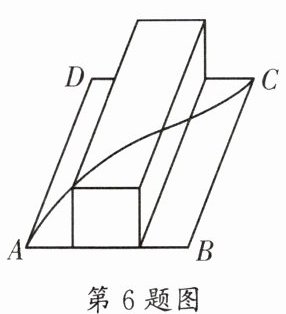
10

答案： 解：将木块侧面展开，使A、C两点所在平面共面。此时，长方形草坪的长AD=6米，宽AB=4米，木块横截面为边长2米的正方形，展开后横向总长度为6米，纵向总长度为4+2=6米。根据勾股定理，最短路程为$\sqrt{6^{2}+8^{2}}=10$米。
答案：10

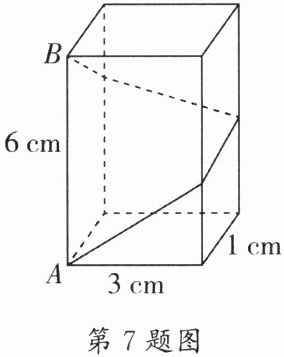
7. (双流区期末)如图,长方体的底面边长分别为1cm和3cm,高为6cm。如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要10cm；如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要$2\sqrt{9 + 16n^{2}}$cm。

答案： 将长方体侧面展开，底面周长为$2×(1 + 3)=8\,\text{cm}$，高为$6\,\text{cm}$。
缠绕一圈时，细线最短路径为展开矩形的对角线，长度为$\sqrt{8^{2}+6^{2}}=\sqrt{64 + 36}=\sqrt{100}=10\,\text{cm}$。
缠绕$n$圈时，底面展开长度为$8n\,\text{cm}$，最短路径为$\sqrt{(8n)^{2}+6^{2}}=\sqrt{64n^{2}+36}=2\sqrt{16n^{2}+9}\,\text{cm}$。
10；$2\sqrt{9 + 16n^{2}}$