第95页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
7. (2024·甘南州)某小组8名学生的中考体育分数单位(分)如下:39,40,40,42,42,42,43,44,则该组数据的众数、中位数分别为(
A. 40,42
B. 42,43
C. 42,42
D. 42,41
C
)A. 40,42
B. 42,43
C. 42,42
D. 42,41
答案:
C
8. (2024·广东)数据5,2,5,4,3的众数是
5
.
答案:
5
9. (2024·新疆)学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入到复试环节,参加了口语表达、写作能力两项测试,成绩如表:
|项目\\应试者|口语表达|写作能力|
|--|--|--|
|甲|80|90|
|乙|90|80|
学校规定口语表达按70%,写作能力按30%计入总成绩,根据总成绩择优录取.通过计算,你认为______

|项目\\应试者|口语表达|写作能力|
|--|--|--|
|甲|80|90|
|乙|90|80|
学校规定口语表达按70%,写作能力按30%计入总成绩,根据总成绩择优录取.通过计算,你认为______
乙
同学将被录取.
答案:
乙
10. (2024·西藏)甲、乙、丙三名学生参加仰卧起坐体育项目测试,他们一周测试成绩的平均数相同,方差如下:$s_{甲}^{2}=1.5,s_{乙}^{2}=3.4,s_{丙}^{2}=0.9$,则甲、乙、丙中成绩最稳定的学生是______
丙
.
答案:
丙
11. 一组数据2,4,a,7,7的平均数$\overline {x}=5$,则方差$s^{2}=$
3.6
.
答案:
3.6
12. 如果一组数据为4,a,5,3,8,其平均数为a,那么这组数据的方差为
$\frac{14}{5}$
.
答案:
$\frac{14}{5}$
13. 现有甲、乙两种糖果的单价与千克数如下表所示.| |甲种糖果|乙种糖果||--|--|--||单价(元/千克)|30|20||千克数|2|3|将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为
24
元/千克.
答案:
24
14. (2024·河南)为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.
|队员|平均每场得分|平均每场篮板|平均每场失误|
|--|--|--|--|
|甲|26.5|8|2|
|乙|26|10|3|
根据以上信息,回答下列问题.
(1) 这六场比赛中,得分更稳定的队员是______
(2) 请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好。(注:答案不唯一,合理即可)
(3) 规定“综合得分”为:平均每场得分$×1+$平均每场篮板$×1.5+$平均每场失误$×(-1)$,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
甲的综合得分为:$26.5×1 + 8×1.5 + 2×(-1) = 36.5$。乙的综合得分为:$26×1 + 10×1.5 + 3×(-1) = 38$。因为 $38 > 36.5$,所以乙队员表现更好。
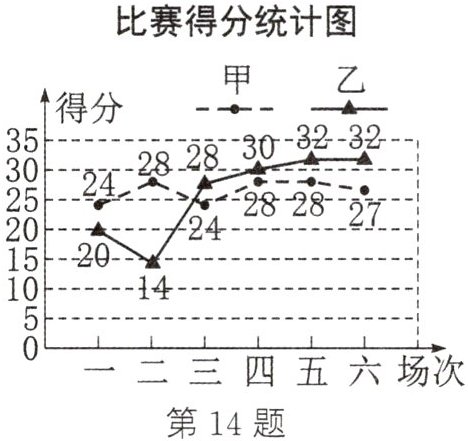
|队员|平均每场得分|平均每场篮板|平均每场失误|
|--|--|--|--|
|甲|26.5|8|2|
|乙|26|10|3|
根据以上信息,回答下列问题.
(1) 这六场比赛中,得分更稳定的队员是______
甲
______(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为______29
______分.(2) 请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好。(注:答案不唯一,合理即可)
(3) 规定“综合得分”为:平均每场得分$×1+$平均每场篮板$×1.5+$平均每场失误$×(-1)$,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
甲的综合得分为:$26.5×1 + 8×1.5 + 2×(-1) = 36.5$。乙的综合得分为:$26×1 + 10×1.5 + 3×(-1) = 38$。因为 $38 > 36.5$,所以乙队员表现更好。

答案:
(1) 甲,29
(2) 因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好。(注:答案不唯一,合理即可);
(3) 甲的综合得分为:$26.5×1 + 8×1.5 + 2×(-1) = 36.5$。乙的综合得分为:$26×1 + 10×1.5 + 3×(-1) = 38$。因为 $38 > 36.5$,所以乙队员表现更好。
(1) 甲,29
(2) 因为甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定,所以甲队员表现更好。(注:答案不唯一,合理即可);
(3) 甲的综合得分为:$26.5×1 + 8×1.5 + 2×(-1) = 36.5$。乙的综合得分为:$26×1 + 10×1.5 + 3×(-1) = 38$。因为 $38 > 36.5$,所以乙队员表现更好。
查看更多完整答案,请扫码查看


