《2025年高效精练九年级数学上册苏科版》

6. 为响应市委市政府提出的建设“绿色城市”的号召,我市某单位准备将院内一块长 $ 30 \mathrm{m} $,宽 $ 20 \mathrm{m} $ 的长方形空地,建成一个矩形花园. 要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为 $ 532 \mathrm{m}^2 $,那么小道进出口的宽度应为多少? (注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

设小道进出口的宽度应为xm,根据题意,得(30 - 2x)(20 - x) = 532。整理,得x² - 35x + 34 = 0。解得x1 = 34(舍去),x2 = 1。所以进出口宽度为1m。

答案： 设小道进出口的宽度应为xm,根据题意,得(30 - 2x)(20 - x) = 532。整理,得x² - 35x + 34 = 0。解得x1 = 34(舍去),x2 = 1。所以进出口宽度为1m。

7. 在一面高度为 $ 2.8 \mathrm{m} $ 的墙上,准备开凿一个矩形窗户,现用 $ 9.5 \mathrm{m} $ 长的铝合金制成如图所示的窗框,则窗户的宽和高各是多少时,其透光面积为 $ 3 \mathrm{m}^2 $(铝合金的宽度忽略不计)?

窗户的宽为2m，高为1.5m时，其透光面积为 $ 3 \mathrm{m}^2 $。

答案： 设窗户的高为(x + 0.5)m,则窗户的宽为$\frac{9.5 - 2x - 1.5}{3}$m,即为$\frac{8 - 2x}{3}$m。根据题意得(x + 0.5)×$\frac{8 - 2x}{3}$ = 3。整理得2x² - 7x + 5 = 0。解得x1 = 1,x2 = 2.5。检验:当x2 = 2.5时,x + 0.5 = 3 ＞ 2.8,舍去。所以x = 1,x + 0.5 = 1.5(m),$\frac{8 - 2x}{3}$ = 2(m)。
∴窗户的高为1.5m,宽为2m时，其透光面积为3m²。

8. 为了倡导节能低碳的生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过 a 千瓦·时,则一个月的电费为 20 元;若超过 a 千瓦·时,则除了交 20 元外,超过部分每千瓦·时要交 $ \frac{a}{100} $ 元. 某宿舍 3 月份用电 80 千瓦·时,交电费 35 元;4 月份用电 45 千瓦·时,交电费 20 元.
(1) 求 a 的值;
(2) 若该宿舍 5 月份交电费 45 元,那么该宿舍当月用电量为多少千瓦·时?

答案：
(1) 根据3月份用电80千瓦·时，交电费35元，得，20 + $\frac{a}{100}$(80 - a) = 35,即a² - 80a + 1500 = 0。解得a = 30或a = 50。由4月份用电45千瓦·时,交电费20元,得，a ≥ 45。
∴a = 50。
(2) 设月用电量为x千瓦·时，交电费y元，则y = $\begin{cases}20(0\leq x\leq50)\\20 + 0.5(x - 50)(x ＞ 50)\end{cases}$。
∵5月份交电费45元,
∴5月份用电量超过50千瓦·时。
∴45 = 20 + 0.5(x - 50),解得x = 100。答:若该宿舍5月份交电费45元,那么该宿舍当月用电量为100千瓦·时。

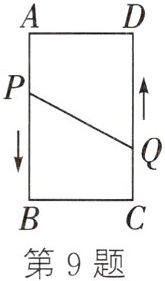
9. 如图,矩形 ABCD 中,$ AB = 16 \mathrm{cm} $,$ AD = 6 \mathrm{cm} $,动点 P,Q 分别从点 A,C 同时出发,点 P 以 $ 3 \mathrm{cm}/\mathrm{s} $ 的速度向点 B 移动,一直到达 B 为止,点 Q 以 $ 2 \mathrm{cm}/\mathrm{s} $ 的速度向 D 移动.
(1) P,Q 两点从出发开始到几秒时,四边形 PBCQ 的面积为 $ 33 \mathrm{cm}^2 $?
(2) P,Q 两点从出发开始到几秒时,点 P 和点 Q 的距离是 $ 10 \mathrm{cm} $?

答案：

(1) 设P,Q两点从出发开始到x秒时四边形PBCQ的面积为33cm²,则PB = (16 - 3x)cm,QC = 2xcm,根据梯形的面积公式得$\frac{1}{2}$(16 - 3x + 2x)×6 = 33,解之得x = 5。
(2) 设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,过点Q作QE⊥AB,垂足为E,如图,则QE = AD = 6,PQ = 10,
∵PA = 3t,CQ = BE = 2t,
∴PE = AB - AP - BE = |16 - 5t|,由勾股定理,得(16 - 5t)² + 6² = 10²,解得t1 = 4.8,t2 = 1.6。
答:
(1) P,Q两点从出发开始到5秒时四边形PBCQ的面积为33cm²。
(2) 从出发到1.6秒或4.8秒时，点P和点Q的距离是10cm。