《2025年高效精练九年级数学上册苏科版》

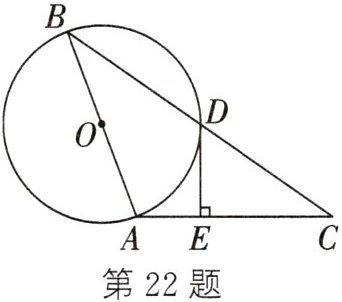
22. (2023·东营)如图，在$\triangle ABC$中，$AB=AC$，以AB为直径的$\odot O$交BC于点D，$DE\perp AC$，垂足为E.
(1) 求证：DE是$\odot O$的切线；
(2) 若$\angle C=30^{\circ }$，$CD=2\sqrt {3}$，求$\overset{\frown }{BD}$的长为$\frac{2\pi}{3}$.

答案： $(1)$ 证明$DE$是$\odot O$的切线
- **步骤一：连接$OD$
因为$AB = AC$，所以$\angle B=\angle C$。
又因为$OB = OD$（同圆半径相等），所以$\angle B=\angle ODB$，则$\angle ODB=\angle C$。
- **步骤二：证明$OD// AC$
由$\angle ODB=\angle C$，根据同位角相等，两直线平行，可得$OD// AC$。
- **步骤三：证明$OD\perp DE$
因为$DE\perp AC$，即$\angle DEC = 90^{\circ}$，又$OD// AC$，根据两直线平行，同位角相等，可得$\angle ODE=\angle DEC = 90^{\circ}$，即$OD\perp DE$。
- **步骤四：得出结论
因为$OD$是$\odot O$的半径，且$OD\perp DE$，根据切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线，所以$DE$是$\odot O$的切线。
$(2)$ 求$\overset{\frown }{BD}$的长
- **步骤一：求$\angle BOD$的度数
连接$AD$，因为$AB$是$\odot O$的直径，所以$\angle ADB = 90^{\circ}$（直径所对的圆周角是直角）。
又因为$AB = AC$，所以$BD = CD = 2\sqrt{3}$（等腰三角形三线合一）。
已知$\angle C = 30^{\circ}$，则$\angle B=\angle C = 30^{\circ}$，$\angle BOD = 2\angle B=60^{\circ}$（同弧所对的圆心角是圆周角的$2$倍）。
- **步骤二：求$OB$的长度
在$Rt\triangle ABD$中，$\angle B = 30^{\circ}$，$BD = 2\sqrt{3}$，根据$\cos B=\frac{BD}{AB}$，可得$AB=\frac{BD}{\cos B}=\frac{2\sqrt{3}}{\cos30^{\circ}}=\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}} = 4$，则$OB=\frac{1}{2}AB = 2$。
- **步骤三：根据弧长公式计算$\overset{\frown }{BD}$的长
根据弧长公式$l=\frac{n\pi r}{180}$（其中$n$是圆心角度数，$r$是半径），可得$\overset{\frown }{BD}$的长为$\frac{60\pi×2}{180}=\frac{2\pi}{3}$。
综上，$(1)$ 证明过程如上述；$(2)$$\overset{\frown }{BD}$的长为$\boldsymbol{\frac{2\pi}{3}}$。

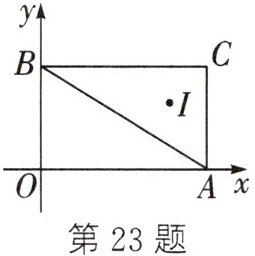
23. 如图，在平面直角坐标系xOy中，$A(4,0)$，$B(0,3)$，$C(4,3)$，I是$\triangle ABC$的内心，将$\triangle ABC$绕原点逆时针旋转$90^{\circ }$后，I的对应点$I'$的坐标为（A）

A. $(-2,3)$
B. $(-3,2)$
C. $(3,-2)$
D. $(2,-3)$

答案： A

24. 如图，正方形ABCD的边长为4，$\odot O$的半径为1.若$\odot O$在正方形ABCD内平移($\odot O$可以与该正方形的边相切)，则点A到$\odot O$上的点的距离的最大值为$ 3 \sqrt { 2 } + 1 $.

答案： $ 3 \sqrt { 2 } + 1 $

25. 如图，把腰长为8的等腰直角三角板OAB的一直角边OA放在直线l上，按顺时针方向在l上转动两次，使得它的斜边转到l上，则直角边OA两次转动所扫过的面积为40π.

答案： $ 40 \pi $

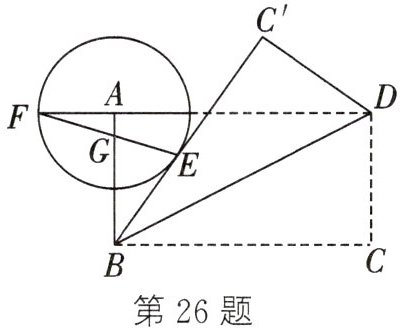
26. (2023·镇江)如图，将矩形ABCD($AD＞AB$)沿对角线BD翻折，C的对应点为点$C'$，以矩形ABCD的顶点A为圆心，r为半径画圆，$\odot A$与$BC'$相切于点E，延长DA交$\odot A$于点F，连接EF交AB于点G.
(1) 求证：$BE=BG$；
(2) 当$r=1$，$AB=2$时，求BC的长.

答案：

(1) 如图，连接 $ A E $，$ \because B C ^ { \prime } $ 与圆相切于 $ E $，$ \therefore $ 半径 $ A E \perp B E $，$ \therefore \angle B E G + \angle A E G = 90 ^ { \circ } $。$ \because $ 四边形 $ A B C D $ 是矩形，$ \therefore \angle B A D = \angle A B C = 90 ^ { \circ } $，$ D C = A B = 2 $，$ \therefore \angle B A F = 90 ^ { \circ } $，$ \therefore \angle A G F + \angle F = 90 ^ { \circ } $。$ \because A F = A E $，$ \therefore \angle F = \angle A E G $，$ \therefore \angle A G F = \angle B E G $。$ \because \angle A G F = \angle B G E $，$ \therefore \angle B E G = \angle B G E $，$ \therefore B E = B G $；
(2) $ \because \angle A E B = 90 ^ { \circ } $，$ A E = 1 $，$ A B = 2 $，$ \therefore \angle A B E = 30 ^ { \circ } $，由折叠的性质得到 $ \angle C B D = \angle D B C ^ { \prime } $，$ \because \angle A B C = 90 ^ { \circ } $，$ \therefore \angle C B D = \frac { 1 } { 2 } \times ( 90 ^ { \circ } - 30 ^ { \circ } ) = 30 ^ { \circ } $，$ \therefore B C = \sqrt { 3 } C D = 2 \sqrt { 3 } $。

27. (2024·山东)如图，在四边形ABCD中，$AD// BC$，$\angle DAB=60^{\circ }$，$AB=BC=2AD=2$.以点A为圆心，以AD为半径作$\overset{\frown }{DE}$交AB于点E，以点B为圆心，以BE为半径作$\overset{\frown }{EF}$所交BC于点F，连接FD交$\overset{\frown }{EF}$于另一点G，连接CG.
(1) 求证：CG为$\overset{\frown }{EF}$所在圆的切线；
(2) 求图中阴影部分面积.(结果保留$\pi$)

(1) 证明：连接BG，
∵$AD// BC$，$AB = BC = 2AD = 2$，∴$AD = 1$，$BE=AB - AE=AB - AD = 2 - 1 = 1$，∴$AD = BE$，
∵$AD// BC$，$AD = BE$，∴四边形$ABED$是平行四边形，
∵$\angle DAB = 60^{\circ}$，$AD = AE = 1$，∴$\triangle ADE$是等边三角形，∴$\angle ADE=\angle DEA = 60^{\circ}$，$DE = AD = 1$，
∴$\angle DEB = 120^{\circ}$，∵$BE = BF = 1$，$AD// BC$，$\angle DAB$与$\angle ABC$互补，$\angle ABC = 120^{\circ}$，$\angle EBF = 60^{\circ}$，∴$\triangle BEF$是等边三角形，∴$\angle BEF=\angle BFE = 60^{\circ}$，$EF = BE = 1$，
∴$DE = EF$，$\angle DEF = 180^{\circ}-\angle DEA-\angle BEF = 60^{\circ}$，∴$\triangle DEF$是等边三角形，∴$\angle EDF = 60^{\circ}$，
∵$BC = 2$，$BF = 1$，∴$CF = BC - BF = 1$，
在$\triangle DCF$中，$DC = 2$，$DF = 1$，$CF = 1$，由余弦定理得$\cos\angle DFC=\frac{DF^{2}+CF^{2}-DC^{2}}{2DF\cdot CF}=\frac{1 + 1 - 4}{2×1×1}=-1$，∴$\angle DFC = 120^{\circ}$，∴$\angle GFC = 60^{\circ}$，
∵$CF = 1$，$\angle GFC = 60^{\circ}$，∴$\triangle CFG$是等边三角形，∴$\angle FCG = 60^{\circ}$，$\angle BCG=\angle BCF-\angle FCG = 30^{\circ}$，$\angle BGC = 180^{\circ}-\angle GBC-\angle BCG = 90^{\circ}$，即$CG\perp BG$，
∵$BG$是$\overset{\frown }{EF}$所在圆的半径，∴CG为$\overset{\frown }{EF}$所在圆的切线；
(2) $\frac{\sqrt{3}}{4}$

答案： $(1)$ 证明$CG$为$\overset{\frown }{EF}$所在圆的切线
本题可通过证明$CG\perp BF$，结合圆的切线判定定理进行证明。
- **步骤一：连接$BG$，分析四边形$ABCD$的性质
已知$AD// BC$，$AB = BC = 2AD = 2$，则$AD = 1$，$BE=AB - AE=AB - AD = 2 - 1 = 1$，所以$AD = BE$。
因为$AD// BC$，$AD = BE$，所以四边形$ABED$是平行四边形。
又因为$\angle DAB = 60^{\circ}$，$AD = AE = 1$，所以$\triangle ADE$是等边三角形，则$\angle ADE=\angle DEA = 60^{\circ}$，$DE = AD = 1$。
所以$\angle DEB = 120^{\circ}$，因为$BE = BF = 1$，$\angle EBF = 60^{\circ}$（$AD// BC$，$\angle DAB$与$\angle ABC$互补，$\angle ABC = 120^{\circ}$，$\angle EBF = 180^{\circ}-\angle ABC = 60^{\circ}$），所以$\triangle BEF$是等边三角形，$\angle BEF=\angle BFE = 60^{\circ}$，$EF = BE = 1$。
所以$DE = EF$，$\angle DEF = 180^{\circ}-\angle DEA-\angle BEF = 60^{\circ}$，则$\triangle DEF$是等边三角形，$\angle EDF = 60^{\circ}$。
- **步骤二：证明$CG\perp BF$
因为$BC = 2$，$BF = 1$，所以$CF = BC - BF = 1$。
在$\triangle DCF$中，$DC = AB = 2$（平行四边形$ABED$中$DE = AB$，$\triangle DEF$是等边三角形，$DF = DE = 1$，$CF = 1$），根据余弦定理$DC^{2}=DF^{2}+CF^{2}-2DF\cdot CF\cdot\cos\angle DFC$，可得$\cos\angle DFC=\frac{DF^{2}+CF^{2}-DC^{2}}{2DF\cdot CF}=\frac{1 + 1 - 4}{2×1×1}=-1$，所以$\angle DFC = 120^{\circ}$，则$\angle GFC = 60^{\circ}$。
因为$BC = 2$，$BF = 1$，$CF = 1$，$\angle GFC = 60^{\circ}$，所以$\triangle CFG$是等边三角形，$\angle FCG = 60^{\circ}$，$\angle BCG=\angle BCF-\angle FCG = 30^{\circ}$，$\angle BGC = 180^{\circ}-\angle GBC-\angle BCG = 90^{\circ}$，即$CG\perp BG$。
因为$BG$是$\overset{\frown }{EF}$所在圆（圆心为$B$）的半径，所以$CG$为$\overset{\frown }{EF}$所在圆的切线。
$(2)$ 求图中阴影部分面积
本题可通过将阴影部分面积转化为$\triangle DFG$的面积减去扇形$BFG$与扇形$AED$的面积差来求解。
- **步骤一：计算$\triangle DFG$的面积
由$(1)$可知$\triangle DEF$是等边三角形，$DF = 1$，$\angle DFG = 60^{\circ}$，$FG = 1$（$\triangle CFG$是等边三角形，$FG = CF = 1$）。
根据三角形面积公式$S=\frac{1}{2}ab\sin C$（$a,b$为三角形两边，$C$为$a,b$夹角），可得${S}_{\triangle DFG}=\frac{1}{2}× DF× FG×\sin\angle DFG=\frac{1}{2}×1×1×\sin60^{\circ}=\frac{\sqrt{3}}{4}$。
- **步骤二：计算扇形$BFG$与扇形$AED$的面积
根据扇形面积公式$S=\frac{n\pi r^{2}}{360}$（$n$为圆心角度数，$r$为半径）。
扇形$BFG$：$n = 60^{\circ}$，$r = 1$，${S}_{扇形BFG}=\frac{60\pi×1^{2}}{360}=\frac{\pi}{6}$。
扇形$AED$：$n = 60^{\circ}$，$r = 1$，${S}_{扇形AED}=\frac{60\pi×1^{2}}{360}=\frac{\pi}{6}$。
- **步骤三：计算阴影部分面积
${S}_{阴影}={S}_{\triangle DFG}-({S}_{扇形BFG}-{S}_{扇形AED})=\frac{\sqrt{3}}{4}-(\frac{\pi}{6}-\frac{\pi}{6})=\boldsymbol{\frac{\sqrt{3}}{4}}$。
综上，$(1)$ 证明如上；$(2)$ 阴影部分面积为$\boldsymbol{\frac{\sqrt{3}}{4}}$。