第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
7. 已知一个三角形的三边长分别为 5,7,8,则其内切圆的半径为 (
A. $\frac { \sqrt { 3 } } { 2 }$
B. $\frac { 3 } { 2 }$
C. $\sqrt { 3 }$
D. $2 \sqrt { 3 }$
C
)A. $\frac { \sqrt { 3 } } { 2 }$
B. $\frac { 3 } { 2 }$
C. $\sqrt { 3 }$
D. $2 \sqrt { 3 }$
答案:
C
8. 如图,$\triangle ABC$内心为 I,连接 AI 并延长交$\triangle ABC$的外接圆于 D,则线段 DI 与 DB 的关系是 (

A. $DI=DB$
B. $DI>DB$
C. $DI<DB$
D. 不确定
A
)
A. $DI=DB$
B. $DI>DB$
C. $DI<DB$
D. 不确定
答案:
A
9. (2023·广元)如图,$∠ACB=45^{\circ }$,半径为 2 的$\odot O$与角的两边相切,点 P 是$\odot O$上任意一点,过点 P 向角的两边作垂线,垂足分别为 E,F,设$t=PE+\sqrt { 2 } P F$,则 t 的取值范围是
2$\sqrt{2}$ ≤ t ≤ 4 + 2$\sqrt{2}$
.
答案:
2$\sqrt{2}$ ≤ t ≤ 4 + 2$\sqrt{2}$
10. 如图,点 E 是$\triangle ABC$的内心,AE 的延长线和$\triangle ABC$的外接圆相交于点 D.
(1) 求证:$BD=DE$;
(2) 连接 OD 交 BC 于点 G,若$OD⊥BC,DG=2,BC=10$,求圆的半径.
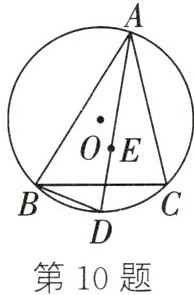
(1) 求证:$BD=DE$;
(2) 连接 OD 交 BC 于点 G,若$OD⊥BC,DG=2,BC=10$,求圆的半径.

答案:
(1) 如图,连接BE,
∵点E是△ABC的内心,
∴∠ABE = ∠CBE,∠BAD = ∠DAC。
∵∠CAD = ∠CBD,
∴∠BAD = ∠DBC,
∴∠DBE = ∠DBC + ∠EBC。
∵∠DEB = ∠ABE + ∠BAD,
∴∠DBE = ∠DEB,
∴BD = DE;
(2) 连接OD,OB,由
(1)可知,∠BAD = ∠DAC,
∴$\overparen{BD}$ = $\overparen{CD}$,
∴OD垂直平分BC,
∴BG = $\frac{1}{2}$BC = $\frac{1}{2}$×10 = 5,设OD = OB = x,则OG = x - DG = x - 2,在Rt△OBG中,由勾股定理可得:OG² + BG² = OB²,
∴(x - 2)² + 5² = x²,解得x = $\frac{29}{4}$,
∴圆的半径为 $\frac{29}{4}$。
(1) 如图,连接BE,
∵点E是△ABC的内心,
∴∠ABE = ∠CBE,∠BAD = ∠DAC。
∵∠CAD = ∠CBD,
∴∠BAD = ∠DBC,
∴∠DBE = ∠DBC + ∠EBC。
∵∠DEB = ∠ABE + ∠BAD,
∴∠DBE = ∠DEB,
∴BD = DE;
(2) 连接OD,OB,由
(1)可知,∠BAD = ∠DAC,
∴$\overparen{BD}$ = $\overparen{CD}$,
∴OD垂直平分BC,
∴BG = $\frac{1}{2}$BC = $\frac{1}{2}$×10 = 5,设OD = OB = x,则OG = x - DG = x - 2,在Rt△OBG中,由勾股定理可得:OG² + BG² = OB²,
∴(x - 2)² + 5² = x²,解得x = $\frac{29}{4}$,
∴圆的半径为 $\frac{29}{4}$。

11. (2024·亭湖区期中)【习题再现】
(教材 P74 第 10 题)如图 1,I 是$\triangle ABC$的内心,AI 的延长线交$\triangle ABC$的外接圆于点 D. BD 和 ID 相等吗? 为什么? (不需解答,请看下面的问题)
【逆向思考】
(1) 如图 1,I 为$\triangle ABC$内一点,AI 的延长线交$\triangle ABC$的外接圆于点 D. 若$DB=DI=DC$,求证:I 为$\triangle ABC$的内心;
【拓展提高】
(2) 如图 2,$\odot O$的半径长为 5,弦$BC=8$,动点 A 在优弧$\overparen { B A C }$上(不与 B,C 重合),I 是$\triangle ABC$的内心.
① 点 I 到$\odot O$上某点的距离始终不变,请用无刻度的直尺找出该点;
② AI 的最大值的______.
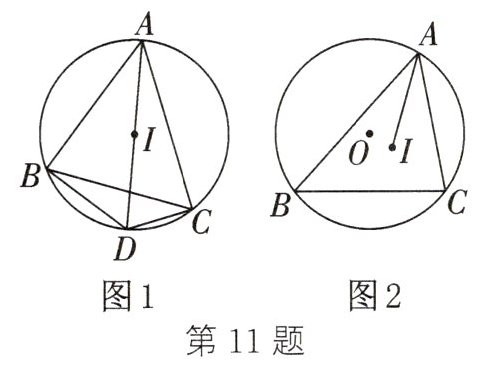
(教材 P74 第 10 题)如图 1,I 是$\triangle ABC$的内心,AI 的延长线交$\triangle ABC$的外接圆于点 D. BD 和 ID 相等吗? 为什么? (不需解答,请看下面的问题)
【逆向思考】
(1) 如图 1,I 为$\triangle ABC$内一点,AI 的延长线交$\triangle ABC$的外接圆于点 D. 若$DB=DI=DC$,求证:I 为$\triangle ABC$的内心;
【拓展提高】
(2) 如图 2,$\odot O$的半径长为 5,弦$BC=8$,动点 A 在优弧$\overparen { B A C }$上(不与 B,C 重合),I 是$\triangle ABC$的内心.
① 点 I 到$\odot O$上某点的距离始终不变,请用无刻度的直尺找出该点;
② AI 的最大值的______.

答案:
(1) 如图1,连接IB,
∵DB = DI = DC,
∴∠DBI = ∠DIB,$\overparen{DB}$ = $\overparen{DC}$,
∴∠DAB = ∠DAC。
∵∠DBC = ∠DAC,
∴∠DBC = ∠DAB。
∵∠DBI = ∠IBC + ∠DBC,∠DIB = ∠IBA + ∠DAB,
∴∠IBC + ∠DBC = ∠IBA + ∠DAB,
∴∠IBC = ∠IBA,
∴点I是△ABC中∠BAC的平分线与∠ABC的平分线的交点,
∴I为△ABC的内心。
(2) ①如图2,延长AI交⊙O于点M,点M就是所求的点。理由:连接BI,BM,CM,
∵I是△ABC的内心,
∴∠MAB = ∠MAC,∠IBC = ∠IBA,
∴$\overparen{MB}$ = $\overparen{MC}$,
∴M为$\overparen{BC}$的中点,
∴MB的长为定值。
∵∠MBC = ∠MAC,
∴∠MBC = ∠MAB,
∴∠MBI = ∠MBC + ∠IBC = ∠MAB + ∠IBA = ∠MIB,
∴MI = MB,
∴点I到⊙O上的点M的距离始终不变,
∴点M就是所求的点。
② 10 - 2$\sqrt{5}$。
(1) 如图1,连接IB,
∵DB = DI = DC,
∴∠DBI = ∠DIB,$\overparen{DB}$ = $\overparen{DC}$,
∴∠DAB = ∠DAC。
∵∠DBC = ∠DAC,
∴∠DBC = ∠DAB。
∵∠DBI = ∠IBC + ∠DBC,∠DIB = ∠IBA + ∠DAB,
∴∠IBC + ∠DBC = ∠IBA + ∠DAB,
∴∠IBC = ∠IBA,
∴点I是△ABC中∠BAC的平分线与∠ABC的平分线的交点,
∴I为△ABC的内心。
(2) ①如图2,延长AI交⊙O于点M,点M就是所求的点。理由:连接BI,BM,CM,
∵I是△ABC的内心,
∴∠MAB = ∠MAC,∠IBC = ∠IBA,
∴$\overparen{MB}$ = $\overparen{MC}$,
∴M为$\overparen{BC}$的中点,
∴MB的长为定值。
∵∠MBC = ∠MAC,
∴∠MBC = ∠MAB,
∴∠MBI = ∠MBC + ∠IBC = ∠MAB + ∠IBA = ∠MIB,
∴MI = MB,
∴点I到⊙O上的点M的距离始终不变,
∴点M就是所求的点。
② 10 - 2$\sqrt{5}$。

查看更多完整答案,请扫码查看


