《2025年高效精练九年级数学上册苏科版》

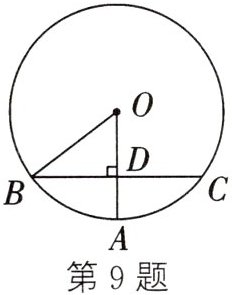
9. (2023·湖州)如图，$OA$是$\odot O$的半径，弦$BC\perp OA$于点$D$，连接$OB$。若$\odot O$的半径为5 cm，$BC$的长为8 cm，则$OD$的长是3cm。

答案： 3

10. (2024·哈尔滨)如图，$AB$是$\odot O$的切线，点$A$为切点，连接$OA$，$OB$，若$\angle OBA=40^{\circ}$，则$\angle AOB=$______50$^{\circ}$。

答案： 50

11. (2024·徐州)如图，$AB$是$\odot O$的直径，点$C$在$AB$的延长线上，$CD$与$\odot O$相切于点$D$，若$\angle C=20^{\circ}$，则$\angle CAD=$______$^{\circ}$。

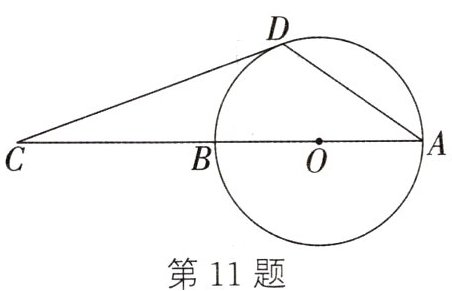
35

答案： 35

12. (2024·齐齐哈尔)若圆锥的底面半径是1 cm，它的侧面展开图的圆心角是直角，则该圆锥的高为$\sqrt{15}$cm。

答案： $\sqrt{15}$

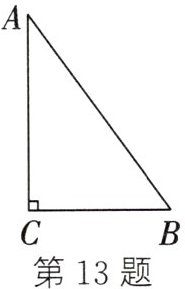
13. (2023·衡阳)如图，在$Rt\triangle ABC$中，$\angle ACB=90^{\circ}$，$AC=8$，$BC=6$。以点$C$为圆心，$r$为半径作圆，当所作的圆与斜边$AB$所在的直线相切时，$r$的值为______$\frac{24}{5}$。

答案： $\frac{24}{5}$

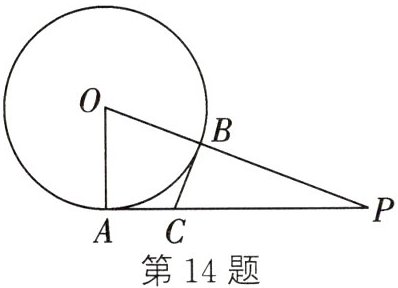
14. (2023·河南)如图，$PA$与$\odot O$相切于点$A$，$PO$交$\odot O$于点$B$，点$C$在$PA$上，且$CB=CA$。若$OA=5$，$PA=12$，则$CA$的长为______$\frac{10}{3}$。

答案： $\frac{10}{3}$

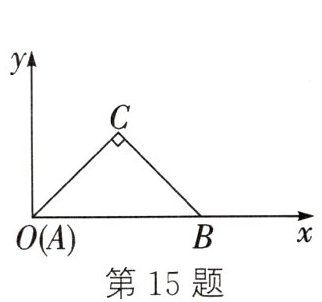
15. 在$Rt\triangle ABC$中，$\angle C=90^{\circ}$，$AC=BC=1$，将其放入平面直角坐标系，使$A$点与原点重合，$AB$在$x$轴上，$\triangle ABC$沿$x$轴顺时针无滑动地滚动，点$A$再次落在$x$轴时停止滚动，则点$A$经过的路线与$x$轴围成图形的面积为$\pi+\frac{1}{2}$。

答案： $\pi+\frac{1}{2}$

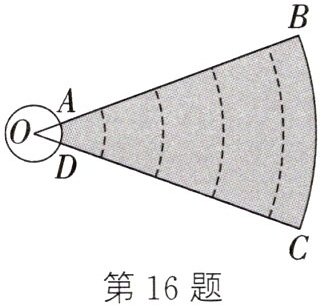
16. (2024·吉林)某新建学校因场地限制，要合理规划体育场地。小明绘制的铅球场地设计图如图所示，该场地由$\odot O$和扇形$OBC$组成，$OB$，$OC$分别与$\odot O$交于点$A$，$D$。$OA=1m$，$OB=10m$，$\angle AOD=40^{\circ}$，则阴影部分的面积为______11π$m^{2}$（结果保留$\pi$）。

答案： $11\pi$

17. (2023·常德)沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”，如图，$\overset{\frown}{AB}$是以$O$为圆心，$OA$为半径的圆弧，$C$是弦$AB$的中点，$D$在$\overset{\frown}{AB}$上，$CD\perp AB$。“会圆术”给出$\overset{\frown}{AB}$长$l$的近似值$s$计算公式：$s=AB+\frac{CD^{2}}{OA}$，当$OA=2$，$\angle AOB=90^{\circ}$时，$|l-s|=$0.1。（结果保留一位小数）

答案： 0.1