第124页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
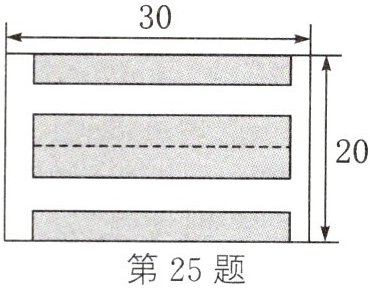
25. (10分)某小区有一块长$30m$,宽$20m$的矩形空地,如图所示.社区计划在这块空地上建一个小型的停车场,阴影部分设计为停车位,其余部分是等宽的通道,已知停车位占地面积为$416m^{2}$.
(1) 求通道的宽是多少米?
(2) 该停车场共有$65$个车位,据调查发现:当每个车位的日租金为$15$元时,可全部租出;当每个车位的日租金每上涨$1$元时,就会少租出$1$个车位.当每个车位的日租金上涨多少元时,既能优惠大众,又能使对外开放的日租金收入为$1200$元?
(1) 通道的宽是
(2) 当每个车位的日租金上涨
(1) 求通道的宽是多少米?
(2) 该停车场共有$65$个车位,据调查发现:当每个车位的日租金为$15$元时,可全部租出;当每个车位的日租金每上涨$1$元时,就会少租出$1$个车位.当每个车位的日租金上涨多少元时,既能优惠大众,又能使对外开放的日租金收入为$1200$元?

(1) 通道的宽是
2
米.(2) 当每个车位的日租金上涨
5
元时,既能优惠大众,又能使对外开放的日租金收入为$1200$元.
答案:
解:
(1) 设通道的宽是 x m,由题意得: $ (30 - 2x)(20 - 2x) = 416 $,整理得 $ x^2 - 25x + 46 = 0 $,解得: $ x_1 = 2 $,$ x_2 = 23 > 20 $ (不合题意舍去),所以通道的宽是 2 m.
(2) 设每个车位的日租金上涨 y 元,则出租的车位为 $ (65 - y) $ 个,由题意得: $ (15 + y)(65 - y) = 1200 $,解得: $ y_1 = 5 $,$ y_2 = 45 $,因为要优惠大众,所以 $ y_2 = 45 $ 舍去. 所以设每个车位的日租金上涨 5 元,既能优惠大众,又能使对外开放的日租金收入为 1200 元.
(1) 设通道的宽是 x m,由题意得: $ (30 - 2x)(20 - 2x) = 416 $,整理得 $ x^2 - 25x + 46 = 0 $,解得: $ x_1 = 2 $,$ x_2 = 23 > 20 $ (不合题意舍去),所以通道的宽是 2 m.
(2) 设每个车位的日租金上涨 y 元,则出租的车位为 $ (65 - y) $ 个,由题意得: $ (15 + y)(65 - y) = 1200 $,解得: $ y_1 = 5 $,$ y_2 = 45 $,因为要优惠大众,所以 $ y_2 = 45 $ 舍去. 所以设每个车位的日租金上涨 5 元,既能优惠大众,又能使对外开放的日租金收入为 1200 元.
26. (12分)在期中复习课里,小晨对九年级数学教材第$52$页习题的第$3$题进行了再研究.
【原题再现】
(1) 如图,在四边形$ABCD$中,$∠A=∠C=90^{\circ }$,经过点$A$,$B$,$D$三点作$\odot O$,点$C$在$\odot O$上吗? 试说明理由.
请你帮他完成后面的解答.
小晨解答如下:
如图1,过$A$,$B$,$D$三点作$\odot O$,连接$AO$,$BO$,$CO$,$DO$.
$\because \odot O$中,$∠BAD=90^{\circ }$,
$\therefore BD$是直径,$\therefore OA=OB=OD$. $\because ∠BCD=90^{\circ }$,$\therefore OC=\frac{1}{2}BD=OB$,$\therefore$点$C$在$\odot O$上
【深入探究】
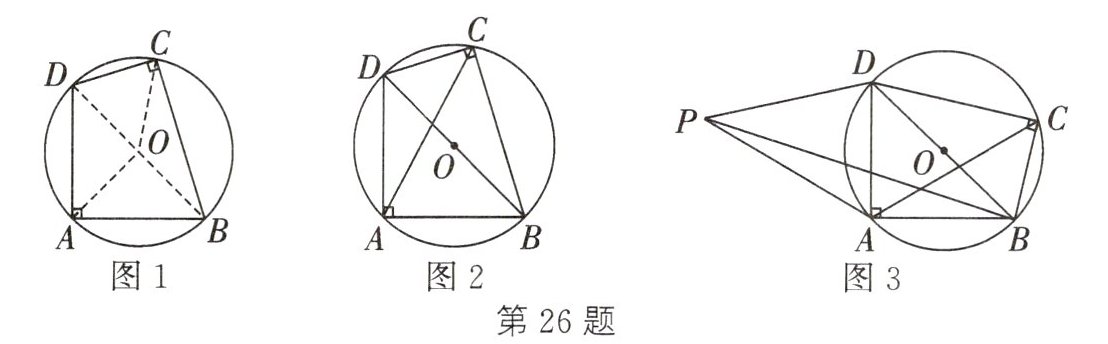
(2) 小晨在完成此题解答后,他在图1上连接$AC$,得到图2,当$AB=AD$时,他发现$CA$平分$∠BCD$.他的发现正确吗? 试说明理由.
(3) 在(2)的条件下,小晨通过测量发现$CD$,$CB$,$CA$这三条线段之间存在着一定的数量关系,经过探究,他得到了结论:$CD+CB=\sqrt {2}CA$,请证明这个结论.
【应用实践】
(4) 根据小晨同学的研究,张老师提出一个问题:如图3,$\odot O$内接四边形$ABCD$中,$BD$为$\odot O$的直径,$AB=AD$,作点$C$关于$AD$的对称点$P$,连接$PA$,$PB$,$PD$,若$PD=6$,$PA=5\sqrt {2}$,请直接写出$PB$的长为
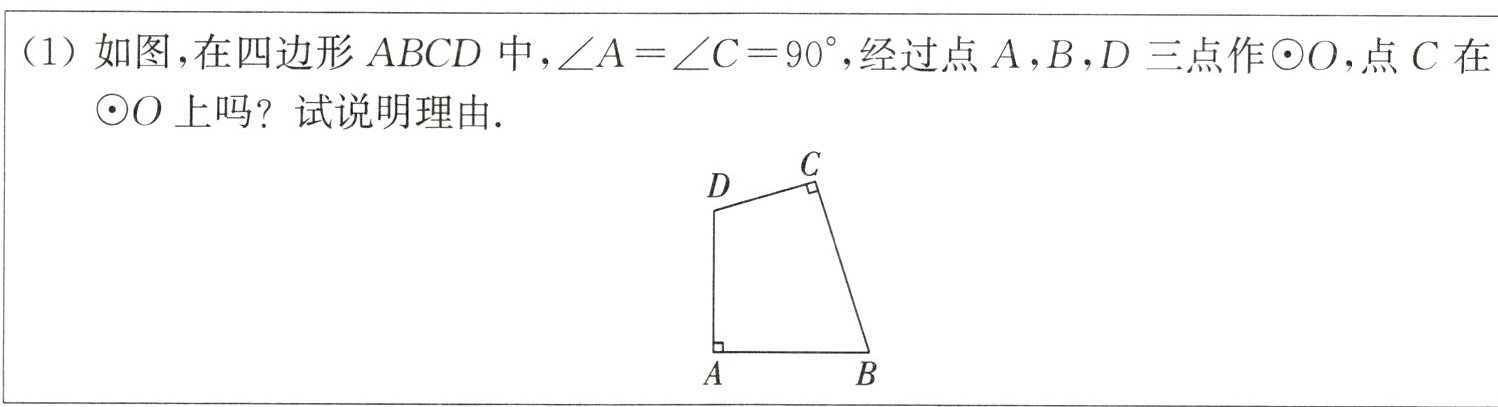
【原题再现】
(1) 如图,在四边形$ABCD$中,$∠A=∠C=90^{\circ }$,经过点$A$,$B$,$D$三点作$\odot O$,点$C$在$\odot O$上吗? 试说明理由.

请你帮他完成后面的解答.
小晨解答如下:
如图1,过$A$,$B$,$D$三点作$\odot O$,连接$AO$,$BO$,$CO$,$DO$.
$\because \odot O$中,$∠BAD=90^{\circ }$,
$\therefore BD$是直径,$\therefore OA=OB=OD$. $\because ∠BCD=90^{\circ }$,$\therefore OC=\frac{1}{2}BD=OB$,$\therefore$点$C$在$\odot O$上
【深入探究】
(2) 小晨在完成此题解答后,他在图1上连接$AC$,得到图2,当$AB=AD$时,他发现$CA$平分$∠BCD$.他的发现正确吗? 试说明理由.
他的发现正确,理由如下: $\because \triangle ABD$中,$∠BAD=90^{\circ }$,$AB=AD$,$\therefore ∠ABD=∠ADB=45^{\circ }$. $\because \odot O$中,$∠ABD=∠ACD$,$∠ADB=∠ACB$,$\therefore ∠ACD=∠ACB$,$\therefore CA$平分$∠BCD$,$\therefore$他的发现正确
(3) 在(2)的条件下,小晨通过测量发现$CD$,$CB$,$CA$这三条线段之间存在着一定的数量关系,经过探究,他得到了结论:$CD+CB=\sqrt {2}CA$,请证明这个结论.
证明: 如图2,延长$CB$至$C'$,使$BC'=CD$,连接$AC'$. $\because$四边形$ABCD$是$\odot O$内接四边形,$\therefore ∠ADC+∠ABC=180^{\circ }$. $\because ∠ABC'+∠ABC=180^{\circ }$,$\therefore ∠ADC=∠ABC'$,又$\because CD=C'B$,$AD=AB$,$\therefore \triangle ADC\cong \triangle ABC'(SAS)$,$\therefore CA=C'A$,$∠DAC=∠BAC'$,$\therefore ∠CAC'=∠CAB+∠BAC'=∠CAB+∠DAC=90^{\circ }$,$\therefore CC'^2=CA^2+C'A^2=2CA^2$,$\therefore CC'=\sqrt{2}CA$. $\because CC'=CB+C'B$,$C'B=CD$,$\therefore CD+CB=\sqrt{2}CA$
【应用实践】
(4) 根据小晨同学的研究,张老师提出一个问题:如图3,$\odot O$内接四边形$ABCD$中,$BD$为$\odot O$的直径,$AB=AD$,作点$C$关于$AD$的对称点$P$,连接$PA$,$PB$,$PD$,若$PD=6$,$PA=5\sqrt {2}$,请直接写出$PB$的长为
$2\sqrt{34}$
.
答案:
(1) 解: 点 C 在 $ \odot O $ 上,理由如下: 如图 1,过 A,B,D 三点作 $ \odot O $,连接 AO,BO,CO,DO. $ \because \odot O $ 中,$ \angle BAD = 90^\circ $,$\therefore BD $ 是直径,$\therefore OA = OB = OD $. $ \because \angle BCD = 90^\circ $,$\therefore OC = \frac{1}{2}BD = OB $,$\therefore $ 点 C 在 $ \odot O $ 上;
(2) 解: 他的发现正确,理由如下: $ \because \triangle ABD $ 中,$ \angle BAD = 90^\circ $,$ AB = AD $,$\therefore \angle ABD = \angle ADB = 45^\circ $. $ \because \odot O $ 中,$ \angle ABD = \angle ACD $,$ \angle ADB = \angle ACB $,$\therefore \angle ACD = \angle ACB $,$\therefore CA $ 平分 $ \angle BCD $,$\therefore $ 他的发现正确;
(3) 证明: 如图 2,延长 CB 至 $ C' $,使 $ BC' = CD $,连接 $ AC' $. $ \because $ 四边形 ABCD 是 $ \odot O $ 内接四边形,$\therefore \angle ADC + \angle ABC = 180^\circ $. $ \because \angle ABC' + \angle ABC = 180^\circ $,$\therefore \angle ADC = \angle ABC' $,又 $ \because CD = C'B $,$ AD = AB $,$\therefore \triangle ADC \cong \triangle ABC' (SAS) $,$\therefore CA = C'A $,$ \angle DAC = \angle BAC' $,$\therefore \angle CAC' = \angle CAB + \angle BAC' = \angle CAB + \angle DAC = 90^\circ $,$\therefore CC'^2 = CA^2 + C'A^2 = 2CA^2 $,$\therefore CC' = \sqrt{2}CA $. $ \because CC' = CB + C'B $,$ C'B = CD $,$\therefore CD + CB = \sqrt{2}CA $;
(4) 解: 延长 BA 至点 Q,使 $ AQ = AB $,连接 DQ,CQ,如图 3,$ \because $ 点 C 关于 AD 的对称点 P,$\therefore AP = AC = 5\sqrt{2} $,$ CD = PD = 6 $,$ \angle PAD = \angle CAD $,$\therefore \triangle PAB \cong \triangle CAQ (SAS) $,$\therefore PB = CQ $. 由
(3) 的结论可知,$ CD + BC = \sqrt{2}AC $,$\therefore 6 + BC = \sqrt{2} \times 5\sqrt{2} $,$\therefore BC = 4 $. $ \because \angle DAB = \angle DAQ = 90^\circ $,$ AD = AD $,$\therefore \triangle ADQ \cong \triangle ADB (SAS) $,$\therefore \angle DQB = \angle DBQ = 45^\circ $,$ DQ = DB $,$\therefore \angle BDQ = 90^\circ $. 过点 Q 作 $ QE \perp CD $ 交 CD 的延长线于点 E,$ \because \angle EQD + \angle EDQ = 90^\circ $,$ \angle BDC + \angle EDQ = 90^\circ $,$\therefore \angle EQD = \angle BDC $. $ \because \angle QED = \angle BCD = 90^\circ $,$\therefore \triangle QED \cong \triangle DCB (AAS) $,$\therefore QE = CD = 6 $,$\therefore CE = 6 + 4 = 10 $,$\therefore PB = CQ = \sqrt{QE^2 + CE^2} = 2\sqrt{34} $. 故答案为: $ 2\sqrt{34} $.
(1) 解: 点 C 在 $ \odot O $ 上,理由如下: 如图 1,过 A,B,D 三点作 $ \odot O $,连接 AO,BO,CO,DO. $ \because \odot O $ 中,$ \angle BAD = 90^\circ $,$\therefore BD $ 是直径,$\therefore OA = OB = OD $. $ \because \angle BCD = 90^\circ $,$\therefore OC = \frac{1}{2}BD = OB $,$\therefore $ 点 C 在 $ \odot O $ 上;
(2) 解: 他的发现正确,理由如下: $ \because \triangle ABD $ 中,$ \angle BAD = 90^\circ $,$ AB = AD $,$\therefore \angle ABD = \angle ADB = 45^\circ $. $ \because \odot O $ 中,$ \angle ABD = \angle ACD $,$ \angle ADB = \angle ACB $,$\therefore \angle ACD = \angle ACB $,$\therefore CA $ 平分 $ \angle BCD $,$\therefore $ 他的发现正确;
(3) 证明: 如图 2,延长 CB 至 $ C' $,使 $ BC' = CD $,连接 $ AC' $. $ \because $ 四边形 ABCD 是 $ \odot O $ 内接四边形,$\therefore \angle ADC + \angle ABC = 180^\circ $. $ \because \angle ABC' + \angle ABC = 180^\circ $,$\therefore \angle ADC = \angle ABC' $,又 $ \because CD = C'B $,$ AD = AB $,$\therefore \triangle ADC \cong \triangle ABC' (SAS) $,$\therefore CA = C'A $,$ \angle DAC = \angle BAC' $,$\therefore \angle CAC' = \angle CAB + \angle BAC' = \angle CAB + \angle DAC = 90^\circ $,$\therefore CC'^2 = CA^2 + C'A^2 = 2CA^2 $,$\therefore CC' = \sqrt{2}CA $. $ \because CC' = CB + C'B $,$ C'B = CD $,$\therefore CD + CB = \sqrt{2}CA $;
(4) 解: 延长 BA 至点 Q,使 $ AQ = AB $,连接 DQ,CQ,如图 3,$ \because $ 点 C 关于 AD 的对称点 P,$\therefore AP = AC = 5\sqrt{2} $,$ CD = PD = 6 $,$ \angle PAD = \angle CAD $,$\therefore \triangle PAB \cong \triangle CAQ (SAS) $,$\therefore PB = CQ $. 由
(3) 的结论可知,$ CD + BC = \sqrt{2}AC $,$\therefore 6 + BC = \sqrt{2} \times 5\sqrt{2} $,$\therefore BC = 4 $. $ \because \angle DAB = \angle DAQ = 90^\circ $,$ AD = AD $,$\therefore \triangle ADQ \cong \triangle ADB (SAS) $,$\therefore \angle DQB = \angle DBQ = 45^\circ $,$ DQ = DB $,$\therefore \angle BDQ = 90^\circ $. 过点 Q 作 $ QE \perp CD $ 交 CD 的延长线于点 E,$ \because \angle EQD + \angle EDQ = 90^\circ $,$ \angle BDC + \angle EDQ = 90^\circ $,$\therefore \angle EQD = \angle BDC $. $ \because \angle QED = \angle BCD = 90^\circ $,$\therefore \triangle QED \cong \triangle DCB (AAS) $,$\therefore QE = CD = 6 $,$\therefore CE = 6 + 4 = 10 $,$\therefore PB = CQ = \sqrt{QE^2 + CE^2} = 2\sqrt{34} $. 故答案为: $ 2\sqrt{34} $.
查看更多完整答案,请扫码查看


