第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
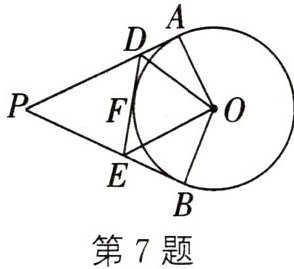
7. 如图,$∠APB=52^{\circ },PA,PB,DE$都为$\odot O$的切线,切点分别为$A,B,F$,且$PA=6$.求:
(1)$△PDE$的周长;
(2)$∠DOE$的度数.
(1)$△PDE$的周长;
(2)$∠DOE$的度数.

答案:
(1)
∵ PA,PB,DE 都为⊙O 的切线,
∴ DA = DF,EB = EF,PA = PB = 6,
∴ DE = DA + EB,
∴ PE + PD + DE = PA + PB = 12,即△PDE 的周长为 12;
(2) 如图,连接OF,
∵ PA,PB,DE 分别切⊙O 于 A,B,F 三点,
∴ OB⊥PB,OA⊥PA,∠BOE = ∠FOE = $\frac{1}{2}$∠BOF,∠FOD = ∠AOD = $\frac{1}{2}$∠AOF.
∵ ∠APB = 52°,
∴ ∠AOB = 360° - 90° - 90° - 52° = 128°,
∴ ∠DOE = ∠FOE + ∠FOD = $\frac{1}{2}$(∠BOF + ∠AOF) = $\frac{1}{2}$∠AOB = 64°.

(1)
∵ PA,PB,DE 都为⊙O 的切线,
∴ DA = DF,EB = EF,PA = PB = 6,
∴ DE = DA + EB,
∴ PE + PD + DE = PA + PB = 12,即△PDE 的周长为 12;
(2) 如图,连接OF,
∵ PA,PB,DE 分别切⊙O 于 A,B,F 三点,
∴ OB⊥PB,OA⊥PA,∠BOE = ∠FOE = $\frac{1}{2}$∠BOF,∠FOD = ∠AOD = $\frac{1}{2}$∠AOF.
∵ ∠APB = 52°,
∴ ∠AOB = 360° - 90° - 90° - 52° = 128°,
∴ ∠DOE = ∠FOE + ∠FOD = $\frac{1}{2}$(∠BOF + ∠AOF) = $\frac{1}{2}$∠AOB = 64°.

8. (2024·滨州)刘徽(今山东滨州人)是魏晋时期我国伟大的数学家,中国古典数学理论的奠基者之一,被誉为“世界古代数学泰斗”.刘徽在注释《九章算术》时十分重视一题多解,其中最典型的是勾股容方和勾股容圆公式的推导,他给出了内切圆直径的多种表达形式.如图,$Rt△ABC$中,$∠C=90^{\circ },AB,BC,CA$的长分别为$c,a,b$.则可以用含$c,a,b$的式子表示出$△ABC$的内切圆直径$d$,下列表达式错误的是 (
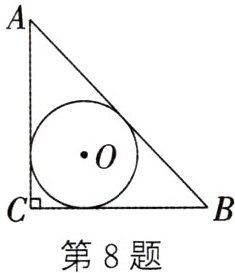
A. $d=a+b-c$
B. $d=\frac {2ab}{a+b+c}$
C. $d=\sqrt {2(c-a)(c-b)}$
D. $d=|(a-b)(c-b)|$
D
)
A. $d=a+b-c$
B. $d=\frac {2ab}{a+b+c}$
C. $d=\sqrt {2(c-a)(c-b)}$
D. $d=|(a-b)(c-b)|$
答案:
D
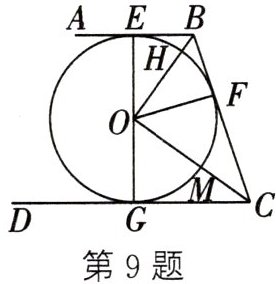
9. 如图,$AB,BC,CD$分别与$\odot O$相切于$E,F,G$,且$AB// CD,BO=6,CO=8$.
(1) 判断$△OBC$的形状,并证明你的结论;
(2) 求$\odot O$的半径$OF$的长.
(1) 判断$△OBC$的形状,并证明你的结论;
直角三角形
(2) 求$\odot O$的半径$OF$的长.
4.8

答案:
(1) △OBC 是直角三角形. 证明:
∵ AB,BC,CD 分别与⊙O 相切于 E,F,G,
∴ ∠OBE = ∠OBF = $\frac{1}{2}$∠EBF,∠OCG = ∠OCF = $\frac{1}{2}$∠GCF.
∵ AB//CD,
∴ ∠EBF + ∠GCF = 180°,
∴ ∠OBF + ∠OCF = 90°,
∴ ∠BOC = 90°,
∴ △OBC 是直角三角形;
(2)
∵ 在 Rt△BOC 中,BO = 6,CO = 8,
∴ BC = $\sqrt{BO^{2} + CO^{2}}$ = 10.
∵ AB,BC,CD 分别与⊙O 相切于 E,F,G,
∴ OF⊥BC,
∴ OF = $\frac{BO×CO}{BC}$ = $\frac{6×8}{10}$ = 4.8.
(1) △OBC 是直角三角形. 证明:
∵ AB,BC,CD 分别与⊙O 相切于 E,F,G,
∴ ∠OBE = ∠OBF = $\frac{1}{2}$∠EBF,∠OCG = ∠OCF = $\frac{1}{2}$∠GCF.
∵ AB//CD,
∴ ∠EBF + ∠GCF = 180°,
∴ ∠OBF + ∠OCF = 90°,
∴ ∠BOC = 90°,
∴ △OBC 是直角三角形;
(2)
∵ 在 Rt△BOC 中,BO = 6,CO = 8,
∴ BC = $\sqrt{BO^{2} + CO^{2}}$ = 10.
∵ AB,BC,CD 分别与⊙O 相切于 E,F,G,
∴ OF⊥BC,
∴ OF = $\frac{BO×CO}{BC}$ = $\frac{6×8}{10}$ = 4.8.
10. 如图,$AB$为$\odot O$直径,$PA,PC$分别与$\odot O$相切于点$A,C,PQ⊥PA,PQ$交$OC$的延长线于点$Q$.
(1) 求证:$OQ=PQ$;
(2) 连$BC$并延长交$PQ$于点$D,PA=AB$,且$CQ=6$,求$BD$的长.
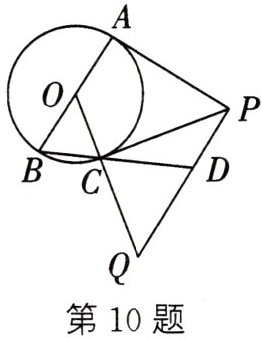
(1) 连接OP. ∵ PA,PC 分别与⊙O 相切于点 A,C,∴ PA = PC,OA⊥PA. ∵ OA = OC,OP = OP,∴ △OPA ≌ △OPC(SSS),∴ ∠AOP = ∠POC. ∵ QP⊥PA,∴ QP//BA,∴ ∠QPO = ∠AOP,∴ ∠QOP = ∠QPO,∴ OQ = PQ;
(2) 设 OA = r. ∵ OB = OC,∴ ∠OBC = ∠OCB. ∵ OB//QD,∴ ∠QDC = ∠B. ∵ ∠OCB = ∠QCD,∴ ∠QCD = ∠QDC,∴ QC = QD = 6. ∵ QO = QP,∴ OC = DP = r. ∵ PC 是⊙O 的切线,∴ OC⊥PC,PC = PA = AB = 2r,∴ ∠OCP = ∠PCQ = 90°,在 Rt△PCQ 中,∵ PQ² = PC² + QC²,∴ (6 + r)² = (2r)² + 6²,r = 4 或 0(舍弃),∴ OP = $\sqrt{4^{2} + 8^{2}}$ = 4$\sqrt{5}$,∵ OB = PD,OB//PD,∴ 四边形 OBDP 是平行四边形,∴ BD = OP =
(1) 求证:$OQ=PQ$;
(2) 连$BC$并延长交$PQ$于点$D,PA=AB$,且$CQ=6$,求$BD$的长.
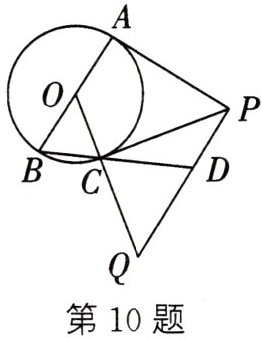
(1) 连接OP. ∵ PA,PC 分别与⊙O 相切于点 A,C,∴ PA = PC,OA⊥PA. ∵ OA = OC,OP = OP,∴ △OPA ≌ △OPC(SSS),∴ ∠AOP = ∠POC. ∵ QP⊥PA,∴ QP//BA,∴ ∠QPO = ∠AOP,∴ ∠QOP = ∠QPO,∴ OQ = PQ;
(2) 设 OA = r. ∵ OB = OC,∴ ∠OBC = ∠OCB. ∵ OB//QD,∴ ∠QDC = ∠B. ∵ ∠OCB = ∠QCD,∴ ∠QCD = ∠QDC,∴ QC = QD = 6. ∵ QO = QP,∴ OC = DP = r. ∵ PC 是⊙O 的切线,∴ OC⊥PC,PC = PA = AB = 2r,∴ ∠OCP = ∠PCQ = 90°,在 Rt△PCQ 中,∵ PQ² = PC² + QC²,∴ (6 + r)² = (2r)² + 6²,r = 4 或 0(舍弃),∴ OP = $\sqrt{4^{2} + 8^{2}}$ = 4$\sqrt{5}$,∵ OB = PD,OB//PD,∴ 四边形 OBDP 是平行四边形,∴ BD = OP =
4$\sqrt{5}$
.
答案:
(1) 连接OP.
∵ PA,PC 分别与⊙O 相切于点 A,C,
∴ PA = PC,OA⊥PA.
∵ OA = OC,OP = OP,
∴ △OPA ≌ △OPC(SSS),
∴ ∠AOP = ∠POC.
∵ QP⊥PA,
∴ QP//BA,
∴ ∠QPO = ∠AOP,
∴ ∠QOP = ∠QPO,
∴ OQ = PQ;
(2) 设 OA = r.
∵ OB = OC,
∴ ∠OBC = ∠OCB.
∵ OB//QD,
∴ ∠QDC = ∠B.
∵ ∠OCB = ∠QCD,
∴ ∠QCD = ∠QDC,
∴ QC = QD = 6.
∵ QO = QP,
∴ OC = DP = r.
∵ PC 是⊙O 的切线,
∴ OC⊥PC,PC = PA = AB = 2r,
∴ ∠OCP = ∠PCQ = 90°,在 Rt△PCQ 中,
∵ PQ² = PC² + QC²,
∴ (6 + r)² = (2r)² + 6²,r = 4 或 0(舍弃),
∴ OP = $\sqrt{4^{2} + 8^{2}}$ = 4$\sqrt{5}$,
∵ OB = PD,OB//PD,
∴ 四边形 OBDP 是平行四边形,
∴ BD = OP = 4$\sqrt{5}$.
(1) 连接OP.
∵ PA,PC 分别与⊙O 相切于点 A,C,
∴ PA = PC,OA⊥PA.
∵ OA = OC,OP = OP,
∴ △OPA ≌ △OPC(SSS),
∴ ∠AOP = ∠POC.
∵ QP⊥PA,
∴ QP//BA,
∴ ∠QPO = ∠AOP,
∴ ∠QOP = ∠QPO,
∴ OQ = PQ;
(2) 设 OA = r.
∵ OB = OC,
∴ ∠OBC = ∠OCB.
∵ OB//QD,
∴ ∠QDC = ∠B.
∵ ∠OCB = ∠QCD,
∴ ∠QCD = ∠QDC,
∴ QC = QD = 6.
∵ QO = QP,
∴ OC = DP = r.
∵ PC 是⊙O 的切线,
∴ OC⊥PC,PC = PA = AB = 2r,
∴ ∠OCP = ∠PCQ = 90°,在 Rt△PCQ 中,
∵ PQ² = PC² + QC²,
∴ (6 + r)² = (2r)² + 6²,r = 4 或 0(舍弃),
∴ OP = $\sqrt{4^{2} + 8^{2}}$ = 4$\sqrt{5}$,
∵ OB = PD,OB//PD,
∴ 四边形 OBDP 是平行四边形,
∴ BD = OP = 4$\sqrt{5}$.
查看更多完整答案,请扫码查看


