第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
10. 如图,正方形 $ A B C D $ 的外接圆为 $ \odot O $,点 $ P $ 在劣弧 $ \overparen { C D } $ 上(不与 $ C $ 点重合).
(1) 求 $ \angle B P C $ 的度数;
(2) 若 $ \odot O $ 的半径为 8,求正方形 $ A B C D $ 的边长.
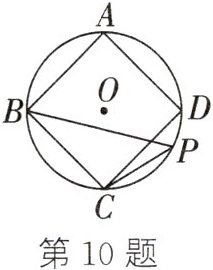
(1) 求 $ \angle B P C $ 的度数;
45°
(2) 若 $ \odot O $ 的半径为 8,求正方形 $ A B C D $ 的边长.
8√2

答案:
(1) 连接 $OB$, $OC$,
∵ 四边形 $ABCD$ 为正方形,
∴ $∠BOC = 90^{\circ}$,
∴ $∠BPC = \frac{1}{2}∠BOC = 45^{\circ}$;
(2) 过点 $O$ 作 $OE⊥BC$ 于点 $E$,
∵ $OB = OC$, $∠BOC = 90^{\circ}$,
∴ $∠OBE = 45^{\circ}$,
∴ $OE = BE$,
∵ $OE^{2} + BE^{2} = OB^{2}$,
∴ $BE = \sqrt{\frac{OB^{2}}{2}} = \sqrt{\frac{64}{2}} = 4\sqrt{2}$,
∴ $BC = 2BE = 2×4\sqrt{2} = 8\sqrt{2}$.
(1) 连接 $OB$, $OC$,
∵ 四边形 $ABCD$ 为正方形,
∴ $∠BOC = 90^{\circ}$,
∴ $∠BPC = \frac{1}{2}∠BOC = 45^{\circ}$;
(2) 过点 $O$ 作 $OE⊥BC$ 于点 $E$,
∵ $OB = OC$, $∠BOC = 90^{\circ}$,
∴ $∠OBE = 45^{\circ}$,
∴ $OE = BE$,
∵ $OE^{2} + BE^{2} = OB^{2}$,
∴ $BE = \sqrt{\frac{OB^{2}}{2}} = \sqrt{\frac{64}{2}} = 4\sqrt{2}$,
∴ $BC = 2BE = 2×4\sqrt{2} = 8\sqrt{2}$.
11. (2024·东营)我国魏晋时期数学家刘徽在《九章算术注》中提到著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少. 割之又割,以至于不可割,则与圆周合体,而无所失矣”. “割圆术”孕育了微积分思想,他用这种思想得到了圆周率 $ \pi $ 的近似值为 3.1416,如图, $ \odot O $ 的半径为 1,运用“割圆术”,以圆内接正六边形面积近似估计 $ \odot O $ 的面积,可得 $ \pi $ 的估计值为 $ \frac { 3 \sqrt { 3 } } { 2 } $,若用圆内接正八边形近似估计 $ \odot O $ 的面积,可得 $ \pi $ 的估计值为______
$2\sqrt{2}$
.
答案:
$2\sqrt{2}$
12. (2023·衡阳)如图,用若干个全等的正五边形排成圆环状,图中所示的是其中 3 个正五边形的位置. 要完成这一圆环排列,共需要正五边形的个数是______

10
.
答案:
10
13. 如图,正六边形 $ A B C D E F $ 为 $ \odot O $ 的内接正六边形.
(1) 若 $ \odot O $ 的半径为 $ 4 \mathrm { cm } $,求正六边形 $ A B C D E F $ 的周长和面积.周长为
(2) 点 $ G $ 在 $ \overparen { C D } $ 上, $ C G $ 恰好是 $ \odot O $ 内接正十边形的一边, $ D G $ 恰好是 $ \odot O $ 内接正 $ n $ 边形的一边,求 $ n $.$n=$
(1) 若 $ \odot O $ 的半径为 $ 4 \mathrm { cm } $,求正六边形 $ A B C D E F $ 的周长和面积.周长为
24
cm,面积为24√3
cm².(2) 点 $ G $ 在 $ \overparen { C D } $ 上, $ C G $ 恰好是 $ \odot O $ 内接正十边形的一边, $ D G $ 恰好是 $ \odot O $ 内接正 $ n $ 边形的一边,求 $ n $.$n=$
15
.
答案:
(1) 连接 $OC$, $OD$,
∵ 六边形 $ABCDEF$ 是圆内接正六边形,
∴ $∠COD = \frac{360^{\circ}}{6} = 60^{\circ}$.
∵ $OC = OD$,
∴ $△COD$ 是正三角形,
∴ $CD = OC = OD = 4 (cm)$,
∴ 正六边形 $ABCDEF$ 的周长为 $4×6 = 24 (cm)$.
∵ $S_{\triangle COD} = \frac{1}{2}×4×2\sqrt{3} = 4\sqrt{3} (cm^{2})$,
∴ $S_{\text{正六边形}ABCDEF} = 6S_{\triangle COD} = 24\sqrt{3} (cm^{2})$, 答: 正六边形 $ABCDEF$ 的周长为 $24 cm$, 面积为 $24\sqrt{3} cm^{2}$;
(2) 连接 $OG$,
∵ $CG$ 是正十边形的边长,
∴ $∠COG = \frac{360^{\circ}}{10} = 36^{\circ}$,
∴ $∠DOG = ∠COD - ∠COG = 60^{\circ} - 36^{\circ} = 24^{\circ}$.
∵ $DG$ 是圆内接正 $n$ 边形的边长,
∴ $\frac{360^{\circ}}{n} = 24^{\circ}$, 解得 $n = 15$.
(1) 连接 $OC$, $OD$,
∵ 六边形 $ABCDEF$ 是圆内接正六边形,
∴ $∠COD = \frac{360^{\circ}}{6} = 60^{\circ}$.
∵ $OC = OD$,
∴ $△COD$ 是正三角形,
∴ $CD = OC = OD = 4 (cm)$,
∴ 正六边形 $ABCDEF$ 的周长为 $4×6 = 24 (cm)$.
∵ $S_{\triangle COD} = \frac{1}{2}×4×2\sqrt{3} = 4\sqrt{3} (cm^{2})$,
∴ $S_{\text{正六边形}ABCDEF} = 6S_{\triangle COD} = 24\sqrt{3} (cm^{2})$, 答: 正六边形 $ABCDEF$ 的周长为 $24 cm$, 面积为 $24\sqrt{3} cm^{2}$;
(2) 连接 $OG$,
∵ $CG$ 是正十边形的边长,
∴ $∠COG = \frac{360^{\circ}}{10} = 36^{\circ}$,
∴ $∠DOG = ∠COD - ∠COG = 60^{\circ} - 36^{\circ} = 24^{\circ}$.
∵ $DG$ 是圆内接正 $n$ 边形的边长,
∴ $\frac{360^{\circ}}{n} = 24^{\circ}$, 解得 $n = 15$.
查看更多完整答案,请扫码查看


