《2025年教材全解高中数学选择性必修第三册人教版A版》

1. 若$A_m^4 = 18C_m^3$，则$m = ($ )

A.9
B.8
C.7
D.6

答案： 1.D 解析：由A$_{m}^{4}$=18C$_{m}^{3}$，得m(m-1)(m-2)(m-3)=18·$\frac{m(m-1)(m-2)}{3×2×1}$，且m≥4，m∈N*，解得m=6.

2. 现有男、女学生共 8 人，从男生中选 2 人，从女生中选 1 人分别参加数学、物理、化学三科竞赛，共有 90 种不同方案，那么男、女生人数分别是(C)

A.2,6
B.5,3
C.3,5
D.6,2

答案： 2.C 解析：设男生有x人，女生有y人，则$\begin{cases}x+y=8,\\C_{x}^{2}·C_{y}^{1}·A_{3}^{3}=90,\end{cases}$解得x=3,y=5.

3. 用数字 0,1,2,3,4,5 组成没有重复数字的四位数，若将组成的不重复的四位数按从小到大的顺序排成一个数列，则第 85 个数为(A)

A.2 301
B.2 304
C.2 302
D.2 303

答案： 3.A 解析：千位为1的有A$_{5}^{3}$=60个，前两位为20的有A$_{4}^{2}$=12个，前两位为21的有A$_{4}^{2}$=12个，所以第85个数字是前两位为23的最小数，即2301.

4. 已知$(\sqrt{x}+\frac{2}{x^2})^n$的展开式中，第 3 项的系数与倒数第 3 项的系数之比为$\frac{1}{16}$，则展开式中二项式系数最大的项为第(C)项.

A.3
B.4
C.5
D.6

答案： 4.C 解析：$(\sqrt{x}+\frac{2}{x^{2}})^{n}$的展开式的通项公式为T$_{k+1}$=C$_{n}^{k}$·$(\sqrt{x})^{n-k}$·$(\frac{2}{x^{2}})^{k}$=C$_{n}^{k}$·2$^{k}$·x$^{\frac{n-5k}{2}}$，则第3项的系数为C$_{n}^{2}$·2$^{2}$，倒数第3项的系数为C$_{n}^{n-2}$·2$^{n-2}$.因为第3项的系数与倒数第3项的系数之比为$\frac{1}{16}$，所以$\frac{C_{n}^{2}·2^{2}}{C_{n}^{n-2}·2^{n-2}}$=$\frac{1}{16}$=2$^{-4}$，所以C$_{n}^{2}$·2$^{2}$=C$_{n}^{n-2}$·2$^{n-6}$，解得n=8，所以展开式中二项式系数最大的项为第5项．

5. 某校在“数学联赛”考试后选取了 6 名教师参加阅卷，试卷共 4 道解答题，要求将这 6 名教师分成 4 组，每组改一道解答题，其中 2 组各有 2 名教师，另外 2 组各有 1 名教师，则不同的分配方案的种数是(D)

A.216
B.420
C.720
D.1 080

答案： 5.D 解析：6人分成4组共有$\frac{C_{6}^{2}C_{4}^{2}}{2}$种不同的分组方案，所以共有$\frac{C_{6}^{2}C_{4}^{2}}{2}$A$_{4}^{4}$=$\frac{15×6}{2}$×24=1080种分配方案．

6. $(2-\frac{1}{x^2})(1 + ay)^6$展开式中$x^2y^3$项的系数为 160，则$a = ($ )

A.2
B.4
C.-2
D.$-2\sqrt{2}$

答案： 6.C 解析：二项式(1+ay)$^{6}$展开式的通项公式为T$_{k+1}$=C$_{6}^{k}$×1$^{6-k}$(ay)$^{k}$=C$_{6}^{k}$a$^{k}$y$^{k}$，令k=3，可得二项式(1+ay)$^{6}$展开式中y$^{3}$的系数为C$_{6}^{3}$a$^{3}$，所以$(2-\frac{1}{x^{2}})(1+ay)^{6}$展开式中x$^{-2}$y$^{3}$项的系数为(-1)×C$_{6}^{3}$a$^{3}$=160，可得a$^{3}$=-8，解得a=-2.

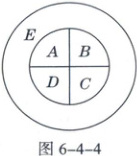
7. 某广场布置了一个如图 6-4-4 所示的圆形花坛，花坛分为 5 个区域. 现有 6 种不同的花卉可供选择，要求相邻的区域(有公共边)不能布置相同的花卉，且每个区域只布置一种花卉，则不同的布置方案有(C)

A.720 种
B.1 440 种
C.1 560 种
D.2 520 种

答案： 7.C 解析：不同的布置方案分两类：当A与C布置相同的花卉时，先安排E，有6种不同的选择；再不安排A与C，有5种不同的选择；再安排B，有4种不同的选择；最后安排D，有4种不同的选择，共有6×5×4×4=480种布置方案．当A与C布置不同的花卉时，先安排E，有6种不同的选择；再安排A与C，有5×4种不同的选择；再安排B，有3种不同的选择；最后安排D，有3种不同的选择，共有6×5×4×3×3=1080种布置方案．所以不同的布置方案有480+1080=1560种．

8. 若$(ax+\frac{b}{x})^6$的展开式中常数项为 160，则$a^2 + b^2$的最小值为(C)

A.$\sqrt{2}$
B.2
C.4
D.8

答案： 8.C 解析：二项式$(ax+\frac{b}{x})^{6}$的展开式的通项公式为 T$_{k+1}$=C$_{6}^{k}$(ax)$^{6-k}$$(\frac{b}{x})^{k}$=a$^{6-k}$b$^{k}$·C$_{6}^{k}$x$^{6-2k}$，令6-2k=0，得k=3，所以a$^{3}$b$^{3}$C$_{6}^{3}$=160，所以ab=2.因为a$^{2}$+b$^{2}$≥2ab=4，当且仅当a=b=$\sqrt{2}$时，等号成立，所以a$^{2}$+b$^{2}$的最小值为4.

9. 下列说法正确的有(CD)

A.某班 4 位同学从文学、经济和科技三类不同的图书中各借 1 本，有不同的借法 64 种
B.用 1,2,3 三个数字可以组成 9 个三位奇数
C.从集合$A = \{a,b,c,d\}$中任取 2 个元素组成集合$B$，则集合$B$中含有元素$b$的概率为$\frac{1}{2}$
D.两个男生和两个女生随机排成一列，则两个女生不相邻的概率是$\frac{1}{2}$

答案： 9.CD 解析：对于A，第1位同学可以从三类不同的图书中任选一类，有3种选法，同理，其他的3位同学也各有3种选法，则不同的选书方法有3×3×3×3=81种，故A错误；对于B，个位可以放1,3，十位和百位都可以放1,2,3，所以可以组成2×3×3=18个奇数，故B错误；对于C，从集合A中任取2个元素可得到集合B的个数为C$_{4}^{2}$，含有b的集合个数为C$_{3}^{1}$，其概率为$\frac{C_{3}^{1}}{C_{4}^{2}}$=$\frac{1}{2}$，故C正确；对于D，两个女生和两个男生随机排成一列，总的排法有A$_{4}^{4}$=24种，两个女生不相邻的排法有A$_{2}^{2}$×A$_{2}^{2}$=12种，所以两个女生不相邻的概率为$\frac{12}{24}$=$\frac{1}{2}$，故D正确．

10. 关于多项式$(1+\frac{2}{x}-x)^6$的展开，下列结论正确的有(BD)

A.各项系数之和为 1
B.各项系数的绝对值之和为$2^{12}$
C.不存在常数项
D.$x^3$的系数为 40

答案： 10.BD 解析：在多项式$(1+\frac{2}{x}-x)^{6}$中，令x=1，可得各项系数之和为2$^{6}$，所以A不正确．多项式$(1+\frac{2}{x}-x)^{6}$展开式的各项系数的绝对值之和与多项式$(1+\frac{2}{x}+x)^{6}$展开式的各项系数之和相等，在多项式$(1+\frac{2}{x}+x)^{6}$中，令x=1，可得各项系数之和为3$^{6}$=729，令x=-1，可得3$^{6}$=1+1+1+⋯+1=729，所以$\vert a_{0}\vert$+$\vert a_{1}\vert$+⋯+$\vert a_{10}\vert$=3$^{10}$-1，故B正确．由$(1+\frac{2}{x}-x)^{6}$=$[(1+\frac{2}{x})-x]^{6}$的展开式的通项公式为T$_{r+1}$=C$_{6}^{r}$$(\frac{2}{x}-x)^{r}$(0≤r≤6,r∈Z)，$(\frac{2}{x}-x)^{r}$的展开式的通项公式为T$_{k+1}$=C$_{r}^{k}$$(\frac{2}{x})^{r-k}$$(-x)^{k}$(0≤k≤r,k∈Z)，当2k-r=0时为常数，所以多项式$(1+\frac{2}{x}-x)^{6}$展开式中有常数项，C不正确．当2k-r=3,0≤k≤r,r,k∈Z时，$\begin{cases} k=3,&\\r=3 \end{cases}$或$\begin{cases} k=4,&\\r=5, \end{cases}$(-1)$^{3}$×C$_{6}^{3}$×C$_{3}^{3}$×2$^{0}$+(-1)$^{4}$×C$_{6}^{5}$×C$_{5}^{4}$×2$^{1}$=40，所以x$^{3}$的系数为40，故D正确．

11. 小兰给自己制定了周一到周六的运动计划，这六天每天安排一项运动，其中有两天练习瑜伽，另外四天的运动项目互不相同，且运动项目为跑步、爬山、打羽毛球和跳绳，下列说法正确的有(BCD)

A.若瑜伽被安排在周一和周六，则共有 48 种不同的安排方法
B.若周二和周五至少有一天安排练习瑜伽，则共有 216 种不同的安排方法
C.若周一不练习瑜伽，周三爬山，则共有 36 种不同的安排方法
D.若瑜伽不被安排在相邻的两天，则共有 240 种不同的安排方法

答案： 11.BCD 解析：对于A，若瑜伽被安排在周一和周六，则共有A$_{4}^{4}$=24种不同的安排方法，A不正确；对于B，若周二和周五至少有一天安排练习瑜伽，则由间接法可得共有A$_{6}^{4}$-A$_{2}^{2}$A$_{4}^{4}$=216种不同的安排方法，B正确；对于C，若周一不练习瑜伽，周三爬山，则共有C$_{1}^{1}$A$_{4}^{4}$=36种不同的安排方法，C正确；对于D，若瑜伽不被安排在相邻的两天，则先排其他四项运动，共有A$_{4}^{4}$种不同的安排方法，再从5个空位里插入2个安排练习瑜伽，共有A$_{4}^{4}$C$_{5}^{2}$=240种不同的安排方法，D正确．

12. 从正方体的 8 个顶点中任选 4 个，则这 4 个点在同一平面的概率为$\frac{6}{35}$.

答案： 12.$\frac{6}{35}$ 解析：从正方体的8个顶点中任选4个，有n=C$_{8}^{4}$=70个结果，这4个点在同一平面的有m=6+6=12个结果，所以所求概率为$\frac{m}{n}$=$\frac{12}{70}$=$\frac{6}{35}$．

13. 若存在$n\in N^*$，使得$(ax + 1)^{2n}$和$(x + a)^{2n + 1}(其中 a\neq0)$的展开式中含$x^n$项的系数相等，则$a$的最大值为$\frac{2}{3}$.

答案： 13.$\frac{2}{3}$ 解析：根据(x+a)$^{2n+1}$的展开式中第k+1项为T$_{k+1}$=C$_{2n+1}^{k+1}$·x$^{2n+1-k-1}$a$^{k+1}$，令2n+1-k=n，得k=n+1，所以含x$^{n}$项的系数为C$_{2n+1}^{n+1}$a$^{n+1}$．同理(ax+1)$^{2n}$的展开式中含x$^{n}$项的系数为C$_{2n}^{n}$a$^{n}$．由C$_{2n+1}^{n+1}$a$^{n+1}$=C$_{2n}^{n}$a$^{n}$，得a=$\frac{n+1}{2n+1}$，又y=$\frac{n+1}{2n+1}$=$\frac{1}{2}$+$\frac{1}{2(2n+1)}$在(0,+∞)上单调递减，n∈N*，所以$\frac{1}{2}$＜a≤$\frac{2}{3}$，故a的最大值为$\frac{2}{3}$．

14. 甲、乙、丙、丁、戊五名同学参加某种技能竞赛，得出了第一名到第五名的五个名次，甲、乙去询问成绩，组织者对甲说：“很遗憾，你和乙都未拿到冠军.”对乙说：“你当然不会是最差的.”从组织者的回答分析，这五个人的名次排列的不同情况共有54种.

答案： 14.54 解析：由题意知，甲、乙都没有得到冠军，且乙不是最后一名，分两种情况讨论：①甲是最后一名，则乙可以是第二名、第三名或第四名，即乙有3种名次排列情况，剩下的三人有A$_{3}^{3}$=6种名次排列情况；②甲不是最后一名，则甲、乙需要排在第二、三、四名，有A$_{3}^{2}$=6种名次排列情况，剩下的三人有A$_{3}^{3}$=6种名次排列情况，此时有6×6=36种名次排列情况．由分类加法计数原理可知，一共有18+36=54种不同的名次排列情况．

15. (13 分)甲、乙、丙、丁四名同学报名参加$A,B,C$三个智力竞赛项目，每个人都要报名参加，且每个人只能报 1 个竞赛项目. 分别求在下列情况下的不同报名方法的种数.
(1) 甲、乙报同一项目，丙不报$A$项目；
(2) 甲不报$A$项目，且$B,C$项目报名的人数相同.

答案： 15.解：
(1)甲、乙报同一项目，可以在A，B，C三个智力竞赛项目中任选一个，有C$_{3}^{1}$种方法，接下来丁可以在A，B，C三个智力竞赛项目中任选一个，有C$_{3}^{1}$种方法，最后丙不报A项目，共有C$_{3}^{1}$种方法，则甲、乙报同一项目，丙不报A项目共有C$_{3}^{1}$×C$_{3}^{1}$×C$_{2}^{1}$=3×3×2=18种报名方法．
(2)由题意，若B，C项目各有一人，先在乙、丙、丁三名同学中任选一人，有C$_{3}^{1}$种方法，此人与甲在B，C项目中全排列，有A$_{2}^{2}$种方法，余下的二人去参加A项目，有1种方法，则有C$_{3}^{1}$×A$_{2}^{2}$×C$_{2}^{2}$=6种报名方法；若B，C项目各有两人，则先给B项目选人，有C$_{3}^{2}$种方法，再给C项目选人，有C$_{2}^{2}$种方法，则有C$_{3}^{2}$×C$_{2}^{2}$=6种．所以甲不报A项目，且B，C项目报名的人数相同的报名方法共有6+6=12种．