《2025年教材全解高中数学选择性必修第三册人教版A版》

例2 [全国Ⅰ卷]从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，由测量结果得如图7-5-11所示的频率分布直方图.

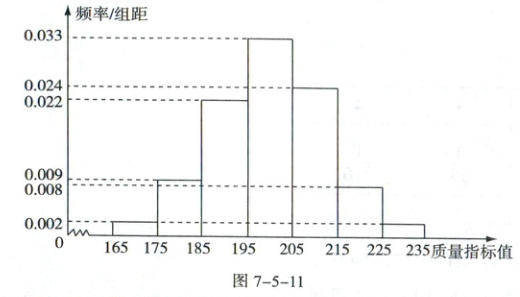
(1)求这500件产品质量指标值的样本平均数$\bar{x}$和样本方差$s^2$(同一组中的数据用该组区间的中点值作代表).
(2)由频率分布直方图可以认为，这种产品的质量指标值$Z$服从正态分布$N(\mu,\sigma^2)$，其中$\mu$近似为样本平均数$\bar{x}$，$\sigma^2$近似为样本方差$s^2$.
①利用该正态分布，求$P(187.8＜Z＜212.2)$；
②某用户从该企业购买了100件这种产品，记$X$表示这100件产品中质量指标值位于区间$(187.8,212.2)$的产品件数，利用①的结果，求$E(X)$.
附：$\sqrt{150}\approx12.2$.
若$Z\sim N(\mu,\sigma^2)$，则$P(\mu - \sigma＜Z＜\mu + \sigma)=0.6826$，$P(\mu - 2\sigma＜Z＜\mu + 2\sigma)=0.9544$.

答案：
(1)
$\begin{aligned}\bar{x}&=170×0.02 + 180×0.09 + 190×0.22 + 200×0.33 + 210×0.24 + 220×0.08 + 230×0.02\\&= 200\\s^2&=(170 - 200)^2×0.02 + (180 - 200)^2×0.09 + (190 - 200)^2×0.22 + (200 - 200)^2×0.33 + (210 - 200)^2×0.24 + (220 - 200)^2×0.08 + (230 - 200)^2×0.02\\&= 150\end{aligned}$
(2)
① $Z\sim N(200,150)$，$\sqrt{150}\approx12.2$，则 $P(187.8\lt Z\lt212.2)=P(200 - 12.2\lt Z\lt200 + 12.2)= 0.6826$。
② 已知一件产品质量指标值位于区间 $(187.8,212.2)$ 的概率为 $0.6826$，$X\sim B(100,0.6826)$，所以 $E(X)=100×0.6826 = 68.26$。

教材第86页例题
李明上学有时坐公交车，有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间，经数据分析得到：坐公交车平均用时30min，样本方差为36；骑自行车平均用时34min，样本方差为4.假设坐公交车用时$X$和骑自行车用时$Y$都服从正态分布.
(1)估计$X$，$Y$的分布中的参数；
(2)根据(1)中的估计结果，利用信息技术工具画出$X$和$Y$的分布密度曲线；
(3)如果某天有38min可用，李明应选择哪种交通工具？如果某天只有34min可用，又应该选择哪种交通工具？请说明理由.

答案：
(1)
对于$X$（坐公交车用时），已知平均用时$\bar{x}=30min$，因为$X$服从正态分布$X\sim N(\mu,\sigma^{2})$，根据正态分布的均值估计，$\hat{\mu}_{X}=\bar{x}=30$，样本方差$s_{x}^{2}=36$，则$\hat{\sigma}_{X}^{2}=s_{x}^{2}=36$，$\hat{\sigma}_{X}=6$，所以$X\sim N(30,6^{2})$。
对于$Y$（骑自行车用时），已知平均用时$\bar{y}=34min$，因为$Y$服从正态分布$Y\sim N(\mu,\sigma^{2})$，根据正态分布的均值估计，$\hat{\mu}_{Y}=\bar{y}=34$，样本方差$s_{y}^{2}=4$，则$\hat{\sigma}_{Y}^{2}=s_{y}^{2}=4$，$\hat{\sigma}_{Y}=2$，所以$Y\sim N(34,2^{2})$。
(2)
利用信息技术工具（如数学软件等），以$x$为横轴，$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x - \mu)^{2}}{2\sigma^{2}}}$为纵轴，分别代入$\mu = 30,\sigma = 6$和$\mu = 34,\sigma = 2$画出$X$和$Y$的分布密度曲线。
(3)
设坐公交车用时不超过$t$分钟的概率为$P(X\leq t)$，骑自行车用时不超过$t$分钟的概率为$P(Y\leq t)$。
当$t = 38$时，
对于$X\sim N(30,6^{2})$，$z_{X}=\frac{38 - 30}{6}=\frac{4}{3}\approx1.33$，查标准正态分布表$P(X\leq38)=\varPhi(1.33)\approx0.9082$。
对于$Y\sim N(34,2^{2})$，$z_{Y}=\frac{38 - 34}{2}=2$，查标准正态分布表$P(Y\leq38)=\varPhi(2)\approx0.9772$。
因为$P(Y\leq38)＞P(X\leq38)$，所以如果某天有$38min$可用，李明应选择骑自行车。
当$t = 34$时，
对于$X\sim N(30,6^{2})$，$z_{X}=\frac{34 - 30}{6}=\frac{2}{3}\approx0.67$，查标准正态分布表$P(X\leq34)=\varPhi(0.67)\approx0.7486$。
对于$Y\sim N(34,2^{2})$，$P(Y\leq34)=0.5$。
因为$P(X\leq34)＞P(Y\leq34)$，所以如果某天只有$34min$可用，李明应选择坐公交车。
综上，答案为：
(1)$X\sim N(30,6^{2})$，$Y\sim N(34,2^{2})$；
(3)有$38min$可用选骑自行车，有$34min$可用选坐公交车。

2-1 [全国Ⅰ卷]为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸(单位：cm).根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布$N(\mu,\sigma^2)$.
(1)假设生产状态正常，记$X$表示一天内抽取的16个零件中其尺寸在$(\mu - 3\sigma,\mu + 3\sigma)$之外的零件数，求$P(X\geq1)$及$X$的数学期望.
(2)一天内抽检零件中，如果出现了尺寸在$(\mu - 3\sigma,\mu + 3\sigma)$之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查维修，试问：上述监控生产过程的方法合理吗？
②下面是检验员在一天内抽取的16个零件的尺寸：
9.95 10.12 9.96 9.96 10.01 9.92
9.98 10.04 10.26 9.91 10.13
10.02 9.22 10.04 10.05 9.95
经计算得$\bar{x}=\frac{1}{16}\sum_{i = 1}^{16}x_i = 9.97$，$s = \sqrt{\frac{1}{16}\sum_{i = 1}^{16}(x_i - \bar{x})^2}=\sqrt{\frac{1}{16}(\sum_{i = 1}^{16}x_i^2 - 16\bar{x}^2)}\approx0.212$，其中$x_i$为抽取的第$i$个零件的尺寸，$i = 1,2,·s,16$.
用样本平均数$\bar{x}$作为$\mu$的估计值$\hat{\mu}$，用样本标准差$s$作为$\sigma$的估计值$\hat{\sigma}$，利用估计值判断是否需对当天的生产过程进行检查？剔除$(\hat{\mu} - 3\hat{\sigma},\hat{\mu} + 3\hat{\sigma})$之外的数据，用剩下的数据估计$\mu$和$\sigma$(精确到0.01).
$0.9973^{16}\approx0.9577$，$\sqrt{0.008}\approx0.09$.

答案： 2-1 解：
(1)抽取的一个零件的尺寸在$(\mu - 3\sigma,\mu + 3\sigma)$之内的概率约为0.9973，从而零件的尺寸在$(\mu - 3\sigma,\mu + 3\sigma)$之外的概率约为0.0027，故$X\sim B(16,0.0027)$。因此$P(X\geqslant1)= 1 - P(X = 0)=1 - 0.9973^{16}\approx1 - 0.9577 = 0.0423$。$X$的数学期望为$E(X)= 16×0.0027 = 0.0432$。
(2)①如果生产状态正常，一个零件尺寸在$(\mu - 3\sigma,\mu + 3\sigma)$之外的概率只有0.0027，一天内抽取的16个零件中，出现尺寸在$(\mu - 3\sigma,\mu + 3\sigma)$之外的零件的概率只有0.0423，发生的概率很小.因此一旦发生这种情况，就有理由认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查，可见上述监控生产过程的方法是合理的.
②由$\overline{x}= 9.97,s\approx0.212$，得$\mu$的估计值为$\hat{\mu}= 9.97,\sigma$的估计值为$\hat{\sigma}= 0.212$，由样本数据可以看出9.22在$(\hat{\mu}- 3\hat{\sigma},\hat{\mu}+ 3\hat{\sigma})$之外，因此需对当天的生产过程进行检查.
剔除数据9.22，剩下数据的平均数为$\frac{1}{15}×(16×9.97 - 9.22)= 10.02$。因为$s=\sqrt{\frac{1}{16}(\sum_{i = 1}^{16}x_{i}^{2}-16\overline{x}^{2})}\approx0.212$，所以$\sum_{i = 1}^{16}x_{i}^{2}\approx16×0.212^{2}+16×9.97^{2}\approx1591.134$，剔除数据9.22，剩下数据的样本方差为$\frac{1}{15}×(1591.134 - 9.22^{2}-15×10.02^{2})\approx0.008$，又$\sqrt{0.008}\approx0.09$，因此$\sigma$的估计值为0.09。