《2025年教材全解高中数学选择性必修第三册人教版A版》

1.[2025·杭州高二检测]从标号分别为1,2,3,4的四个红球和标号分别为1,2,3的三个黑球及标号分别为1,2的两个白球中取出不同颜色的两个小球,不同的取法共有(D)

A.24种
B.9种
C.10种
D.26种

答案： 1.D解析:从三种不同颜色的球中取出不同颜色的两个小球，共有三类情况:第一类,红球+黑球，共有4×3=12种取法;第二类，红球+白球，共有4×2=8种取法;第三类,黑球+白球，共有3×2=6种取法，故取出不同颜色的两个小球共有12+8+6=26种不同的取法.

2.[2025·江苏宿迁高二检测]中国象棋中的“马”在棋盘上是行走“日”字,如图6-1-13所示,可纵走,由A到C,也可横走,由A到D,则“马”由A点到B点的最短走法有(C)

A.4种
B.5种
C.6种
D.7种

答案：
2.C解析:若“马”由A点到B点，则需先到M或N处,如图D - 6 - 2,最少走4步，包含如下路线:
D到N处有2种路线,D到M处有2种路线，C到M处有2种路线，C到N处没有路线，根据分类加法计数原理，最短走法有6种.

3.[2025·山东潍坊高二检测]如果集合$U$存在一组两两不交(两个集合交集为空集时,称为不交)的非空子集$A_1$,$A_2$,$·s$,$A_k(k\in N^*,k\geq2)$,且满足$A_1\cup A_2\cup·s\cup A_k=U$,那么称子集组$A_1$,$A_2$,$·s$,$A_k$构成集合$U$的一个$k$划分.若集合$I$中含有4个元素,则集合$I$的所有划分的个数为(D)

A.7
B.9
C.10
D.14

答案： 3.D解析:要完成的一件事是“确定集合I的所有划分”，不妨设I={1,2,3,4}，分3类完成:
第1类，I的2划分有{1}∪{2,3,4}，{2}∪{1,3,4}，{3}∪{1,2,4}，{4}∪{1,2,3}，{1,2}∪{3,4}，{1,3}∪{2,4}，{1,4}∪{2,3};
第2类，I的3划分有{1,2}∪{3}∪{4}，{1,3}∪{2}∪{4}，{1,4}∪{2}∪{3}，{2,3}∪{1}∪{4}，{2,4}∪{1}∪{3}，{3,4}∪{1}∪{2};
第3类，I的4划分只有{1}∪{2}∪{3}∪{4}.
根据分类加法计数原理，I的划分共有7+6+1=14个.

4.[2025·上海宝山区高二检测]对于定义域为$D$的函数$f(x)$,若对任意的$x_1,x_2\in D$,当$x_1＜x_2$时都有$f(x_1)\leq f(x_2)$,则称函数$f(x)$为“增函数”,若函数$f(x)$的定义域$D = \{ 1,2,3,4,5\}$,值域$A = \{ 6,7,8\}$,则函数$f(x)$为“增函数”的不同函数个数为(C)

A.4
B.5
C.6
D.7

答案： 4.C解析:因为函数f(x)的定义域D={1,2,3,4,5}，值域A={6,7,8}，所以f(x)要满足“增函数”的定义，必有f
(1)=6,f
(5)=8，而元素2,3,4的对应情况分为3类:
第1类，元素2,3,4均与7对应，即f
(2)=f
(3)=f
(4)=7，有1个;
第2类，元素2,3,4中有2个元素与7对应，即f
(2)=f
(3)=7,f
(4)=8，或f
(2)=6,f
(3)=f
(4)=7，有2个;
第3类，元素2,3,4中仅有一个元素与7对应，则有f
(2)=f
(3)=6,f
(4)=7，或f
(2)=6,f
(3)=7,f
(4)=8，或f
(2)=7,f
(3)=f
(4)=8，有3个.
根据分类加法计数原理，函数f(x)为“增函数”的不同函数个数为6.

5.[2025·重庆高二检测]中国灯笼又统称为灯彩,主要有宫灯、纱灯、吊灯等种类.现有4名学生,每人从宫灯、纱灯、吊灯中选购1种,则不同的选购方式有(A)

A.81种
B.64种
C.36种
D.48种

答案： 5.A解析:每名学生都有3种选法，根据分步乘法计数原理，不同的选购方式有$3^4=81$种.

6.从1,2,3,4,5,6,7,8,9这9个数字中任取两个,其中一个作为底数,另一个作为真数,则可以得到不同对数值的个数为(C)

A.64
B.56
C.53
D.51

答案： 6.C解析:由于1只能作为真数，则以1为真数，从其余各数中任取一数为底数，对数值均为0.
从除1外的其余各数中任取两数分别作为对数的底数和真数，共能组成8×7=56个对数式，其中，$\log_24=\log_39$，$\log_22=\log_33$，$\log_23=\log_39$，$\log_32=\log_44$，重复了4次，所以得到不同对数值的个数为1+56 - 4=53.

7.[2025·吉林松原高二检测]10800的不同正因数的个数为(B)

A.70
B.60
C.90
D.80

答案： 7.B解析:因为10800=12×9×10×10=$2^{4}×3^{3}×5^{2}$，所以10800的每个因式分别由m个2，n个3，t个5相乘得到的，其中m∈{0,1,2,3,4}，n∈{0,1,2,3}，t∈{0,1,2}，根据分步乘法计数原理，10800的不同正因数的个数为5×4×3=60.

8.[2025·山东菏泽高二检测]国庆佳节前夕,甲、乙、丙三人从$A,B,C$三个旅游景点中任选一个前去游玩,其中甲到过$A$景点,所以甲不选$A$景点,则不同的选法有(C)

A.12种
B.16种
C.18种
D.24种

答案： 8.C解析:分3步完成，第1步，甲选，有2种选法，第2步，乙选，有3种选法，第3步，丙选，有3种选法，根据分步乘法计数原理，所有的选法有2×3×3=18种.

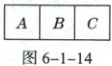
9.[2025·安徽蚌埠高二检测]如图6-1-14所示,用5种不同的颜色对$A,B,C$区域进行着色,要求相邻的区域不能使用同一种颜色,则不同的着色方法共有(C)种.

A.60
B.64
C.80
D.125

答案： 9.C解析:根据给定条件对A,B,C区域进行着色，按用色可以分为2类:
第1类，用2种颜色，则A,C必同色，不同着色方法有5×4=20种;
第2类，用3种颜色，不同着色方法有5×4×3=60种.
根据分类加法计数原理，不同着色方法共有20+60=80种.

10.[2025·河南信阳高二检测]从0,1,2,5中取三个不同的数字,组成能被5整除的三位数,则不同的三位数有(B)

A.12个
B.10个
C.8个
D.7个

答案： 10.B解析:完成的一件事是“从0,1,2,5中取三个不同的数字，组成能被5整除的三位数”，由于能被5整除的三位数末位数字是0或5，因此可分2类完成:
第1类，当末位数字为0时，此时有3×2=6个符合条件的三位数;
第2类，当末位数字为5时，此时有2×2=4个符合条件的三位数.
根据分类加法计数原理，不同的三位数共有4+6=10个.

11.[2025·山东临沂高二检测]集合$A = \{ 1,2,-3\}$,$B = \{ -1,-2,3,4\}$.现从$A,B$中各取一个元素作为点$P(x,y)$的坐标.
(1)可以得到多少个不同的点?
(2)在这些点中,位于第一象限的有几个?

答案： 11.解:
(1)一个点的坐标由x,y两个元素确定，若它们有一个不同，则表示不同的点，又集合A与B中的元素互不相同，所以可分为两类:
第1类:选A中的元素为x，B中的元素为y，有3×4=12个不同的点;
第2类:选A中的元素为y，B中的元素为x，有4×3=12个不同的点.
由分类加法计数原理得不同的点的个数为12+12=24.
(2)第一象限内的点的横、纵坐标都为正数，从而只能取A,B中的正数，又集合A与B中的元素互不相同，所以可分为两类:
第1类:选A中的正元素为x，B中的正元素为y，有2×2=4个不同的点;
第2类:选A中的正元素为y，B中的正元素为x，有2×2=4个不同的点.
由分类加法计数原理得位于第一象限的点的个数为4+4=8.

12.[2025·郑州高二检测][多选题]“二进制”与我国古代的《易经》有着一定的联系,《易经》中有两类最基本的符号:“$—$”和“$--$”,其中“$—$”在二进制中记作1,“$--$”在二进制中记作0,其变化原理与“逢二进一”的法则相通.若从两类符号中任取2个符号排列,则可以组成的不同的十进制数有(BCD)

A.4
B.3
C.2
D.1

答案： 12.BCD解析:从两类符号中任取2个符号排列的情况可分为三类.
第一类:由两个“——”组成，二进制数为11，转化为十进制数为3;
第二类:由两个“——”组成，二进制数为00，转化为十进制数为0;
第三类:由一个“——”和一个“——”组成，二进制数为10,01，转化为十进制数分别为2,1.
所以从两类符号中任取2个符号排列，可以组成的不同的十进制数为0,1,2,3.