《2025年教材全解高中数学选择性必修第三册人教版A版》

例5 某学校组织党史知识竞赛，竞赛规则是：两人组成一个“组合”，进行多轮竞赛，每一轮竞赛中，一个“组合”的两人各答$3$道题，若答对的题目总数不少于$5$道题，此“组合”获得$20$分.已知小华和小夏两人组成“华夏组合”，小华、小夏每道题答对的概率分别是$\frac{4}{5}$和$\frac{3}{4}$，且每道题答对与否互不影响.
(1)求“华夏组合”在一轮竞赛中获得$20$分的概率.
(2)若每轮竞赛互不影响，“华夏组合”期望至少要获得$100$分，则理论上至少要进行多少轮竞赛？

答案：
(1)设小华和小夏答对的题目个数分别为$a_{1}$和$a_{2}$，则所求概率$P = P(a_{1}=2,a_{2}=3)+P(a_{1}=3,a_{2}=2)+P(a_{1}=3,a_{2}=3)$
$\begin{aligned}&=C_{3}^{2}\left(\frac{4}{5}\right)^{2}\left(\frac{1}{5}\right)C_{3}^{3}\left(\frac{3}{4}\right)^{3}+C_{3}^{3}\left(\frac{4}{5}\right)^{3}C_{3}^{2}\left(\frac{3}{4}\right)^{2}\left(\frac{1}{4}\right)+C_{3}^{3}\left(\frac{4}{5}\right)^{3}C_{3}^{3}\left(\frac{3}{4}\right)^{3}\\&=3×\frac{16}{25}×\frac{1}{5}×1×\frac{27}{64}+1×\frac{64}{125}×3×\frac{9}{16}×\frac{1}{4}+1×\frac{64}{125}×1×\frac{27}{64}\\&=\frac{432}{8000}+\frac{1728}{8000}+\frac{1620}{8000}\\&=\frac{3780}{8000}\\&=\frac{297}{500}\end{aligned}$
(2)设进行$n$轮竞赛，得分轮数$X\sim B(n,\frac{297}{500})$，期望$E(X)=n×\frac{297}{500}$。要获得至少$100$分，需$20E(X)\geq100$，即$E(X)\geq5$，则$\frac{297}{500}n\geq5$，$n\geq\frac{2500}{297}\approx8.4$，故$n=9$。
(1)$\frac{297}{500}$；
(2)$9$

例6 小李下班后驾车回家的路线有两条.路线$1$经过三个红绿灯路口，每个路口遇到红灯的概率都是$\frac{1}{3}$；路线$2$经过两个红绿灯路口，第一个路口遇到红灯的概率是$\frac{1}{2}$，第二个路口遇到红灯的概率是$\frac{2}{3}$.假设两条路线全程绿灯时的驾车回家时长相同，且每个红绿灯路口是否遇到红灯相互独立.
(1)若小李下班后选择路线$1$驾车回家，求至少遇到一个红灯的概率.
(2)假设每遇到一个红灯驾车回家时长就会增加$1\min$，为使小李下班后驾车回家时长的累计增加时间(单位：$\min$)的期望最小，小李应选择哪条路线？请说明理由.

答案：
(1)用$X$表示路线1遇到红灯的个数，则$X\sim B(3,\frac{1}{3})$，至少遇到一个红灯的概率$P(X\geq1)=1 - P(X = 0)=1 - C_{3}^{0}(\frac{1}{3})^{0}(1 - \frac{1}{3})^{3}=1 - \frac{8}{27}=\frac{19}{27}$。
(2)路线1。理由：设$Y_{1}$为路线1累计增加时间，$Y_{1}\sim B(3,\frac{1}{3})$，$E(Y_{1})=3×\frac{1}{3}=1$。设$Y_{2}$为路线2累计增加时间，$P(Y_{2}=0)=\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$，$P(Y_{2}=1)=\frac{1}{2}×\frac{2}{3}+\frac{1}{2}×\frac{1}{3}=\frac{1}{2}$，$P(Y_{2}=2)=\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$，$E(Y_{2})=0×\frac{1}{6}+1×\frac{1}{2}+2×\frac{1}{3}=\frac{7}{6}$。因为$1＜\frac{7}{6}$，所以选择路线1。

4-1 [2025·厦门高二检测]将一个半径适当的小球放入如图所示的容器最上方的入口处，小球自由下落，在下落的过程中，小球将遇到黑色障碍物$3$次，最后落入$A$袋或$B$袋中，已知小球每次遇到障碍物时，向左、右两边下落的概率分别是$\frac{1}{3}$，$\frac{2}{3}$.

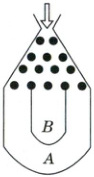
(1)分别求出小球落入$A$袋和$B$袋中的概率；
(2)在容器的入口处依次放入$4$个小球，记$X$为落入$B$袋中的小球的个数，求$X$的分布列、均值和方差.

答案： 解：
(1)设$A=$“小球落入$A$袋”，
$B=$“小球落入$B$袋”，则
$P(A)=\frac{1}{3}×\frac{1}{3}×\frac{1}{3}+\frac{2}{3}×\frac{2}{3}×\frac{2}{3}=\frac{1}{3}$，
所以$P(B)=1-P(A)=1-\frac{1}{3}=\frac{2}{3}$。
(2)$X\sim B\left(4,\frac{2}{3}\right)$，则$X$的分布列为
$P(X=k)=C_{4}^{k}\left(\frac{2}{3}\right)^{k}\left(\frac{1}{3}\right)^{4-k}$
$(k=0,1,2,3,4)$，
即$P(X=0)=\frac{1}{81}$，
$P(X=1)=\frac{8}{81}$，
$P(X=2)=\frac{8}{27}$，
$P(X=3)=\frac{32}{81}$，
$P(X=4)=\frac{16}{81}$
故$X$的分布列为
$X$ 0 1 2 3 4
$P$ $\frac{1}{81}$ $\frac{8}{81}$ $\frac{8}{27}$ $\frac{32}{81}$ $\frac{16}{81}$
$E(X)=4×\frac{2}{3}=\frac{8}{3}$，
$D(X)=4×\frac{2}{3}×\frac{1}{3}=\frac{8}{9}$。

4-2 某百货公司举办了一次有奖促销活动，消费每超过$600$元(含$600$元)，均可抽奖一次，抽奖方案有两种，顾客只能选择其中的一种.方案一：从装有$10$个形状、大小完全相同的小球(其中红球$2$个，白球$1$个，黑球$7$个)的抽奖盒中，一次性摸出$3$个球.其中奖规则为：若摸到$2$个红球和$1$个白球，享受免单优惠；若摸到$2$个红球和$1$个黑球，则打$5$折；若摸到$1$个白球和$2$个黑球，则打$7$折；其余情况不打折.方案二：从装有$10$个形状、大小完全相同的小球(其中红球$3$个，黑球$7$个)的抽奖盒中，有放回地每次摸取$1$球，连摸$3$次，每摸到$1$次红球，立减$200$元.
(1)若两位顾客均消费了$600$元，且均选择抽奖方案一，试求两位顾客均享受免单优惠的概率.
(2)若某顾客消费恰好满$1000$元.
①设该顾客选择抽奖方案一后的实际付款金额为$X$元，求$X$的分布列.
②试比较该顾客选择哪一种抽奖方案更合算.
用$Y_{2}$表示路线$2$累计增加时间，则$Y_{2}$的所有可能取值为$0$，$1$，$2$，
$P(Y_{2}=0)=P(\overline{A}_{1})P(\overline{A}_{2})=\frac{1}{2}×\frac{1}{3}=\frac{1}{6}$，
$P(Y_{2}=1)=P(\overline{A}_{1}A_{2})+P(A_{1}\overline{A}_{2})=\frac{1}{2}×\frac{2}{3}+\frac{1}{2}×\frac{1}{3}=\frac{1}{2}$，
$P(Y_{2}=2)=P(A_{1}A_{2})=\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$，
所以$E(Y_{2})=0×\frac{1}{6}+1×\frac{1}{2}+2×\frac{1}{3}=\frac{7}{6}$.
因为$E(Y_{2})＜E(Y_{1})$，所以小李应选择路线$1$.

答案： 解：
(1)选择方案 若享受到免单优惠，则需要摸出2个红球和1个白球，设顾客享受到免单优惠为事件$A$，
则$P(A)=\frac{C_{2}^{2}C_{8}^{1}}{C_{10}^{3}}=\frac{1}{120}$，
所以两位顾客均享受免单优惠的概
率为$p=P(A)P(A)=\frac{1}{14400}$。
(2)①若选择方案一，且实际付款金额为$X$元，
则$X$可能的取值为0,500,700,1000.
$P(X=0)=\frac{C_{2}^{2}C_{1}^{0}}{C_{10}^{3}}=\frac{1}{120}$，
$P(X=500)=\frac{C_{2}^{2}C_{8}^{1}}{C_{10}^{3}}=\frac{7}{120}$，
$P(X=700)=\frac{C_{2}^{1}C_{8}^{2}}{C_{10}^{3}}=\frac{7}{40}$，
$P(X=1000)=1-\frac{1}{120}-\frac{7}{120}-\frac{7}{40}$
$=\frac{91}{120}$。
故$X$的分布列为
$X$ 0 500 700 1000
$P$ $\frac{1}{120}$ $\frac{7}{120}$ $\frac{7}{40}$ $\frac{91}{120}$
②若选择方案二，设摸到红球的个数为$Y$，付款金额为$Z$元，则$Z=1000-200Y$，由已知可得$Y\sim B\left(3,\frac{3}{10}\right)$
故$E(Y)=3×\frac{3}{10}=\frac{9}{10}$，
所以$E(Z)=E(1000-200Y)$
$=1000-200E(Y)=820$。
由①得，$E(X)=0×\frac{1}{120}+500×\frac{7}{120}+700×\frac{7}{40}+1000×\frac{91}{120}=910$。
因为$E(X)＞E(Z)$，所以该顾客选择第二种抽奖方案更合算.