《2025年教材全解高中数学选择性必修第三册人教版A版》

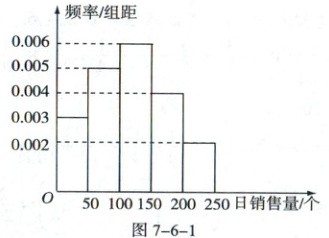
例2II−家面包房根据以往某种面包的销售记录，绘制了日
销售量的频率分布直方图，如图7−6−1所示.

将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立.
(1)求在未来连续3天里，有连续两天的日销售量都不低于100个且另一天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X)

答案：
(1)设$A_1$表示事件“日销售量不低于100个”，$A_2$表示事件“日销售量低于50个”，$B$表示事件“未来连续3天里，有连续两天日销售量不低于100个且另一天日销售量低于50个”。
由频率分布直方图，组距为50，可得：
$P(A_1)=(0.006+0.004+0.002)×50=0.6$，
$P(A_2)=0.003×50=0.15$。
事件$B$包含两种情况：（$A_1,A_1,A_2$）和（$A_2,A_1,A_1$），且每天销售量相互独立，故
$P(B)=P(A_1)P(A_1)P(A_2)+P(A_2)P(A_1)P(A_1)=0.6×0.6×0.15+0.15×0.6×0.6=2×0.6^2×0.15=0.108$。
(2)随机变量$X$表示未来3天里日销售量不低于100个的天数，$X$的可能取值为0,1,2,3，且$X\sim B(3,0.6)$。
$P(X=0)=C_3^0×(1-0.6)^3=1×0.4^3=0.064$，
$P(X=1)=C_3^1×0.6×(1-0.6)^2=3×0.6×0.4^2=0.288$，
$P(X=2)=C_3^2×0.6^2×(1-0.6)=3×0.6^2×0.4=0.432$，
$P(X=3)=C_3^3×0.6^3=1×0.6^3=0.216$。
$X$的分布列为：
| $X$ | 0 | 1 | 2 | 3 |
|-------|-----|------|------|------|
| $P$ | 0.064 | 0.288 | 0.432 | 0.216 |
因为$X\sim B(3,0.6)$，所以
$E(X)=3×0.6=1.8$，
$D(X)=3×0.6×(1-0.6)=0.72$。
答案
(1) $\boxed{0.108}$
(2) 分布列见上表，$E(X)=\boxed{1.8}$，$D(X)=\boxed{0.72}$

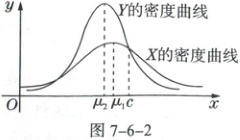
品[多选题青生产红茶已有其年植选用,，在正个环境
下,甲、乙两个品种的茶青每500g的红綦产量(单位:
_
g)分别为X;Y,且X~N(μ,σ²),Y~N(μ2,o²),其密
度曲线如图7−6−2所示，
则以下结论正确的有(ABC)
A.Y的数据较X更集中
B.P(X≤c)＜P(Y≤c)
C.甲种茶青每500g的
红茶产量超过μ的概率大于$\frac{1}{2}$
D.P(X＞c)+P(Y≤c)=1
果研究所制出某种抗病毒菌，为检测其抗病毒效
独立环境下试验一段时间后，确定这些小白鼠的某项
医学指标值X近似服从正态分布N(μ,o²).其中一组
小白鼠该项医学指标直方图(如图7−6−3)的均值与方
差近似为μ和o²,经计算得²=6.920.
(1)若注射该疫苗的小白鼠该项医学指标值不低于
14.77,则认定其体内已经产生抗体,请估计某小白鼠
注射疫苗后产生抗体的概率p(结果精确到0.001);
(2)若图7−6−3是200只小白鼠该项医学指标的直方
图，为了进一步对数据进行分析，从该组医学指标值在
[21,25]的小白鼠中，采用分层抽样的方法随机抽取
10只作为新样本,再从该样本中随机抽取4只小白鼠，
设其医学指标值在[23,25]内的只数为Y;求Y的分布列.
附参考数据:$\sqrt{6.92}$≈2.63.
若X~N(μ,o²),则①P(μ−o≤x≤μ+o)≈0.6827;
②P(μ−2σ≤X≤μ+2σ)≈0.9545;
③P(μ−3σ≤X≤μ+3σ)≈0.9973.
三函数与方程的思想
法有些概率问题常与函薮相结合,如概率公式P((X=
k)=C pk(1−p)n−k,k=0,1,2,,,.,n,可看成k的
函数，也可看成关于概率p的函数，我们应该善于利
用函数思想解决问题，在概率运算过程中，处理参
数求解、期望与方差计算、多个事件的概率求解等
问题时，经常利用题目中的数量关系，把概率问题转
化为相应的方程(组)问题来解决.

答案： 3.ABC 解析：A正确，$Y$的密度曲线更“瘦高”，即数据更集中；
B正确，因为直线$x = c$，$x = \mu_{2}$，$Y$的密度曲线与$x$轴围成的面积$S_{1}$大于直线$x = c$，$x = \mu_{1}$，$X$的密度曲线与$x$轴围成的面积$S_{2}$，又$P(Y \leq c) = \frac{1}{2} + S_{1}$，$P(X \leq c) = \frac{1}{2} + S_{2}$，所以$P(X \leq c) ＜ P(Y \leq c)$；
C正确，因为$\mu_{2} ＜ \mu_{1}$，所以甲种茶青每500g的红茶产量超过$\mu_{2}$的概率$P(X ＞ \mu_{2}) ＞ \frac{1}{2}$；
D错误，由B知$P(X ＞ c) = \frac{1}{2} - S_{2}$，$P(Y \leq c) = \frac{1}{2} + S_{1}$，所以$P(X ＞ c) + P(Y \leq c) = 1 + S_{1} - S_{2} ＞ 1$。
4.解：
(1)$\bar{X} = 0.02 × 12 × 2 + 0.06 × 14 × 2 + 0.14 × 16 × 2 + 0.18 × 18 × 2 + 0.05 × 20 × 2 + 0.03 × 22 × 2 + 0.02 × 24 × 2 = 17.4$，
则$\mu - \sigma \approx 17.4 - 2.63 = 14.77$，所以$P(X \geq \mu - \sigma) \approx \frac{1}{2} × 0.6827 + 0.5 = 0.84135$，
记事件$A$表示小白鼠注射疫苗后产生抗体，则$P(A) = P(X \geq 14.77) \approx 0.841$，
所以估计某小白鼠注射疫苗后产生抗体的概率$p$为0.841。
(2)由频率分布直方图和分层抽样的方法可知，抽取的10只小白鼠中，医学指标值在$[23,25]$内的有4只，在$[21,23)$内的有6只，
所以$Y$的可能取值为0,1,2,3,4.
所以$P(Y = 0) = \frac{C_{6}^{4}}{C_{10}^{4}} = \frac{1}{14}$，
$P(Y = 1) = \frac{C_{6}^{3}C_{4}^{1}}{C_{10}^{4}} = \frac{8}{21}$，
$P(Y = 2) = \frac{C_{6}^{2}C_{4}^{2}}{C_{10}^{4}} = \frac{3}{7}$，
$P(Y = 3) = \frac{C_{6}^{1}C_{4}^{3}}{C_{10}^{4}} = \frac{4}{35}$，
$P(Y = 4) = \frac{C_{4}^{4}}{C_{10}^{4}} = \frac{1}{210}$
所以$Y$的分布列为
$Y$ 0 1 2 3 4
$P$ $\frac{1}{14}$ $\frac{8}{21}$ $\frac{3}{7}$ $\frac{4}{35}$ $\frac{1}{210}$