《2025年教材全解高中数学选择性必修第三册人教版A版》

9.[2025·武汉高二检测]已知随机变量$X \sim B(12,p)$，且$E(2X - 3)=3$，则$D(4X)=$(D)

A.$\frac{9}{4}$
B.$9$
C.$21$
D.$36$

答案： D 解析由随机变量$X \sim B(12,p)$,可得$E(X)=12p$.由$E(2X - 3)=2E(X)-3 = 24p - 3 = 3$,解得$p=\frac{1}{4}$,即$X \sim B\left(12,\frac{1}{4}\right)$,可得$D(X)=12 × \frac{1}{4} × \left(1 - \frac{1}{4}\right)=\frac{9}{4}$,所以$D(4X)=16D(X)=36$.

10. 设随机变量$X \sim B(n,p)$，若二项式$(p + x)^n = a_0 + \frac{1}{2}x + \frac{3}{2}x^2 + ·s + a_n x^n$，则(D)

A.$E(X)=3$，$D(X)=2$
B.$E(X)=4$，$D(X)=2$
C.$E(X)=3$，$D(X)=1$
D.$E(X)=2$，$D(X)=1$

答案： D 解析由题意,可知$(p + x)^{n}=p^{n}+C_{n}^{1}p^{n - 1}x + C_{n}^{2}p^{n - 2}x^{2}+C_{n}^{3}p^{n - 3}x^{3}+·s + C_{n}^{n}x^{n}$.又$(p + x)^{n}=a_{0}+\frac{1}{2}x+\frac{3}{2}x^{2}+·s +a_{n}x^{n}$,所以$\frac{np^{n - 1}}{2}p=\frac{1}{2}$ ①若选项A成立,则$\begin{cases}np = 3,\\np(1 - p)=2,\end{cases}$解得$\begin{cases}n = 9,\\p=\frac{1}{3},\end{cases}$代入①验证不成立,故A错误;若选项B成立,则$\begin{cases}np = 4,\\np(1 - p)=2,\end{cases}$解得$\begin{cases}n = 8,\\p=\frac{1}{2},\end{cases}$代入①验证不成立,故B错误;若选项C成立,则$\begin{cases}np = 3,\\np(1 - p)=1,\end{cases}$解得$\begin{cases}n=\frac{9}{2},\\p=\frac{2}{3},\end{cases}$又$n \notin N^{*}$,不合题意,故C错误;若选项D成立,则$\begin{cases}np = 2,\\np(1 - p)=1,\end{cases}$解得$\begin{cases}n = 4,\\p=\frac{1}{2},\end{cases}$代入①验证成立,故D正确.

11.[多选题]如图7-4-2是一块高尔顿板示意图：在一块木块上钉着若干排互相平行但相互错开的圆柱形小木钉，小木钉之间留有适当的空隙作为通道，前面挡有一块玻璃，将小球从顶端放入，小球在下落过程中，每次碰到小木钉后都等可能地向左或向右落下，最后落入底部的格子中，格子从左到右分别编号为$1,2,3,·s,6$，用$X$表示小球落入口子的号码，则(AD)

A.$P(X=1)=\frac{1}{32}$
B.$E(X)=\frac{5}{2}$
C.当$P$最大时，$X=3$
D.$D(X)=\frac{5}{4}$
]

答案： AD 解析记$A=$“向右下落”,则$\overline{A}=$“向左下落”,且$P(A)=P(\overline{A})=\frac{1}{2}$,令$Y = X - 1$,因为小球最后落人格子的号码$X$等于事件$A$发生的次数$Y$加上$1$,而小球在下落过程中共碰撞小木钉$5$次,则$Y \sim B\left(5,\frac{1}{2}\right)$.对于A,$P(X = 1)=P(Y = 0)=C_{5}^{0} × \left(1 - \frac{1}{2}\right)^{5}=\frac{1}{32}$,故A正确;对于B,$E(X)=E(Y + 1)=E(Y)+1 = 5 × \frac{1}{2}+1=\frac{7}{2}$,故B错误;对于C,$P(X = 1)=P(Y = 0)=C_{5}^{0} × \left(1 - \frac{1}{2}\right)^{5}=\frac{1}{32}$,$P(X = 3)=P(Y = 2)=C_{5}^{2} × \left(\frac{1}{2}\right)^{2} × \left(1 - \frac{1}{2}\right)^{3}=\frac{10}{32}$,$P(X = 4)=P(Y = 3)=C_{5}^{3} × \left(\frac{1}{2}\right)^{3} × \left(1 - \frac{1}{2}\right)^{2}=\frac{10}{32}$,$P(X = 5)=P(Y = 4)=C_{5}^{4} × \frac{1}{2} × \left(1 - \frac{1}{2}\right)^{4}=\frac{5}{32}$,$P(X = 6)=P(Y = 5)=C_{5}^{5} × \left(1 - \frac{1}{2}\right)^{5}=\frac{1}{32}$,故当$X = 3$或$X = 4$时,概率最大,故C错误;对于D,$D(X)=D(Y)=5 × \frac{1}{2} × \left(1 - \frac{1}{2}\right)=\frac{5}{4}$,故D正确.

12.[2024·武汉高三检测][多选题]已知离散型随机变量$X$服从二项分布，即$X \sim B(n,p)$，其中$n \in \mathbb{N}^*,0 ＜ p ＜ 1$，记$X$为奇数的概率为$a$，$X$为偶数的概率为$b$，则下列说法中正确的有(ABC)

A.$a + b = 1$
B.当$p = \frac{1}{2}$时，$a = b$
C.当$0 ＜ p ＜ \frac{1}{2}$时，$a$随着$n$的增大而增大
D.当$\frac{1}{2} ＜ p ＜ 1$时，$a$随着$n$的增大而减小

答案： ABC 解析由概率的基本性质可知,$a + b = 1$,故A正确;当$p=\frac{1}{2}$时,离散型随机变量$X$服从二项分布$B\left(n,\frac{1}{2}\right)$,$P(X = k)=C_{n}^{k} × \left(\frac{1}{2}\right)^{k} × \left(1 - \frac{1}{2}\right)^{n - k}(k = 0,1,2,·s,n)$,$a=\left(\frac{1}{2}\right)^{n} × (C_{n}^{0}+C_{n}^{2}+·s)=\left(\frac{1}{2}\right)^{n} × 2^{n - 1}=\frac{1}{2}$,$b=\left(\frac{1}{2}\right)^{n} × (C_{n}^{0}+C_{n}^{2}+·s)=\left(\frac{1}{2}\right)^{n} × 2^{n - 1}=\frac{1}{2}$,所以$a = b$,故B正确;$a = C_{n}^{0}p(1 - p)+C_{n}^{3}p^{3}(1 - p)^{n - 3}+C_{n}^{5}p^{5}(1 - p)^{n - 5}+·s$,即$a=\frac{[(1 - p)+p]^{n}-[(1 - p)-p]^{n}}{2}=\frac{1-(1 - 2p)^{n}}{2}$,当$0＜p＜\frac{1}{2}$时,$a=\frac{1-(1 - 2p)^{n}}{2}$为正数且$a$随着$n$的增大而增大,故C正确;当$\frac{1}{2}＜p＜1$时,$a=\frac{1-(1 - 2p)^{n}}{2}$正负交替,故D不正确.

13. Poisson分布是常见的离散型概率分布，其概率分布列为$P(X = k)=\frac{\lambda^k}{k!} e^{-\lambda}$，$k = 0,1,2,·s$，其中$e$为自然对数的底数，$\lambda$是Poisson分布的均值. 当二项分布的$n$很大$(n \geq 20)$而$p$很小$(p \leq 0.05)$时，Poisson分布可作为二项分布的近似. 假设每个大肠杆菌基因组含有$10000$个核苷酸对，采用$0.05 J/m^2$紫外线照射大肠杆菌时，每个核苷酸对产生嘧啶二聚体的概率均为$0.0003$，则$\lambda =$3；已知该菌株基因组有一个嘧啶二聚体就致死，则致死率为$1 - e^{-3}$.

答案： 3 $1 - e^{-3}$ 解析由题意得,$n = 10000＞20$,$p = 0.0003＜0.05$,此时Poisson分布可作为二项分布的近似,此时$\lambda = 10000 × 0.0003 = 3$,故不致死的概率$P(X = 0)=\frac{3^{0}}{0!}e^{-3}=e^{-3}$,致死率为$1 - P(X = 0)=1 - e^{-3}$.

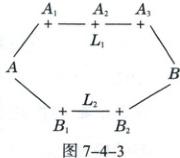
14.[2025·郑州高二检测]王先生家住$A$小区，他工作在$B$科技园区，从家开车到公司上班路上有$L_1,L_2$两条路线(如图7-4-3)，$L_1$路线上有$A_1,A_2,A_3$三个路口，各路口遇到红灯的概率均为$\frac{1}{2}$；$L_2$路线上有$B_1,B_2$两个路口，各路口遇到红灯的概率依次为$\frac{3}{4},\frac{3}{5}$. 若分别走$L_1,L_2$路线，则王先生遇到红灯的次数的均值分别为$\frac{3}{2},\frac{27}{20}$.
]

答案： $\frac{3}{2},\frac{27}{20}$ 解析若走$L_{1}$路线,设王先生遇到红灯的次数为随机变量$X$,则$X \sim B\left(3,\frac{1}{2}\right)$,所以$E(X)=3 × \frac{1}{2}=\frac{3}{2}$;若走$L_{2}$路线,设王先生遇到红灯的次数为随机变量$Y$,则$Y$的取值可以为$0,1,2$,且$P(Y = 0)=\left(1 - \frac{3}{4}\right) × \left(1 - \frac{3}{5}\right)=\frac{1}{10}$,$P(Y = 1)=\frac{3}{4} × \left(1 - \frac{3}{5}\right)+\left(1 - \frac{3}{4}\right) × \frac{3}{5}=\frac{9}{20}$,$P(Y = 2)=\frac{3}{4} × \frac{3}{5}=\frac{9}{20}$,所以$E(Y)=0 × \frac{1}{10}+1 × \frac{9}{20}+2 × \frac{9}{20}=\frac{27}{20}$.

15. 随着科技的不断发展，人工智能技术的应用领域也将会更加广泛，它将会成为改变人类社会发展的重要力量. 某科技公司研发了一套人机交互软件，它会从数据库中检索最贴切的结果进行应答. 在对该交互软件进行测试时，如果输入的问题没有语法错误，则软件正确应答的概率为$80\%$；若出现语法错误，则软件正确应答的概率为$30\%$. 假设每次输入的问题出现语法错误的概率为$10\%$.
(1)求一个问题能被软件正确应答的概率；
(2)在某次测试中，输入了$n(n \geq 6)$个问题，每个问题能否被软件正确应答相互独立，记软件正确应答的个数为$X$，$X = k(k = 0,1,·s,n)$的概率记为$P(X = k)$，则$n$为何值时，$P(X = 6)$的值最大？

答案： 解
(1)记“输入的问题没有语法错误”为事件$A$,“一次正确应答”为事件$B$,由题意$P(\overline{A}) = 0.1$,$P(B|A)=0.8$,$P(B|\overline{A})=0.3$,则$P(A)=1 - P(\overline{A}) = 0.9$,$P(B)=P(AB)+P(\overline{A}B)=P(A)P(B|A)+P(\overline{A})P(B|\overline{A})=0.9 × 0.8 + 0.1 × 0.3 = 0.75$.
(2)依题意,$X \sim B\left(n,\frac{3}{4}\right)$,$P(X = 6)=C_{n}^{6} × \left(\frac{3}{4}\right)^{6} × \left(\frac{1}{4}\right)^{n - 6}$,设$f(n)=C_{n}^{6} × \left(\frac{3}{4}\right)^{6} × \left(\frac{1}{4}\right)^{n - 6}(n \geqslant 6)$,则$\frac{f(n + 1)}{f(n)}=\frac{C_{n + 1}^{6} × \left(\frac{3}{4}\right)^{6} × \left(\frac{1}{4}\right)^{n - 5}}{C_{n}^{6} × \left(\frac{3}{4}\right)^{6} × \left(\frac{1}{4}\right)^{n - 6}}=\frac{n + 1}{4(n - 5)}$,令$\frac{n + 1}{4(n - 5)}＞1$,解得$n＜7$,所以当$n \leqslant 6$时,$f(n + 1)＞f(n)$,令$\frac{n + 1}{4(n - 5)}＜1$,解得$n＞7$,所以当$n \geqslant 8$时,$f(n + 1)＜f(n)$,当$n = 7$时,$f(7)=f(8)$,所以$n = 7$或$n = 8$时,$f(n)$最大,故使$P(X = 6)$最大的$n$的值为$7$或$8$.