《2025年新课程新教材导航学数学九年级上册北师大版》

8. 如图，利用标杆 $ BE $ 测量建筑物的高度. 已知标杆 $ BE $ 高 $ 1.2 $ m，测得 $ AB = 1.6 $ m，$ BC = 12.4 $ m，则建筑物 $ CD $ 的高是（ ）


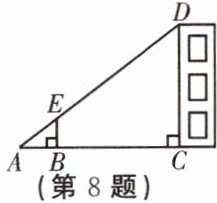
A.$ 9.3 $ m
B.$ 10.5 $ m
C.$ 12.4 $ m
D.$ 14 $ m

答案： 8.B

9. 在一个不透明的袋子里装有若干个红球和 6 个黄球，这些球除颜色外其他都相同. 小明通过多次试验发现，摸出红球的频率稳定在 $ 0.25 $ 左右，则估计袋子中红球的个数是______.

答案： 9.2

10. 如图，在 $ \triangle ABC $ 中，点 $ D $，$ E $ 分别在边 $ AB $，$ AC $ 上，$ DE // BC $，$ AD:DB = 1:2 $，则 $ \triangle ADE $ 与 $ \triangle ABC $ 的面积之比为______.

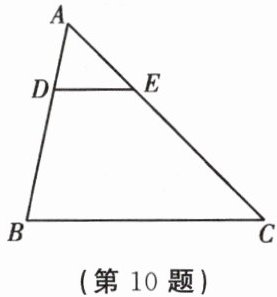
答案： 10.1:9

11. 如图，在矩形 $ ABCD $ 中，$ AB = 10 $，$ AD = 6 $，将矩形 $ ABCD $ 绕点 $ A $ 逆时针旋转一定角度得矩形 $ AB'C'D' $，若点 $ B $ 的对应点 $ B' $ 落在边 $ CD $ 上，则 $ B'C $ 的长为______.

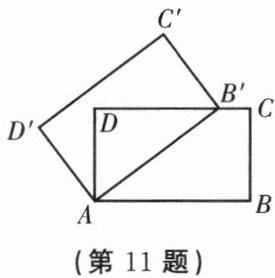
答案： 11.2

12. 已知方程 $ x^{2}+2x - 3 = 0 $ 的解是 $ x_{1} = 1 $，$ x_{2} = -3 $，则方程 $ (2x - 3)^{2}+2(2x - 3)-3 = 0 $ 的解是______.

答案： 12.x₁=2,x₂=0

13. 一个不透明的袋中共有 5 个小球，分别为 2 个红球和 3 个黄球，它们除颜色外其他完全相同. 随机摸出 2 个小球，则摸出的 2 个小球颜色相同的概率为______.

答案： 13.$\frac{2}{5}$

14. 如图，在 $ Rt\triangle ABC $ 中，$ \angle ABC = 90^{\circ} $，$ AB = 3 $，$ BC = 4 $. 在 $ Rt\triangle MPN $ 中，$ \angle MPN = 90^{\circ} $，点 $ P $ 在边 $ AC $ 上，$ PM $ 交边 $ AB $ 于点 $ E $，$ PN $ 交边 $ BC $ 于点 $ F $，当 $ PE = 2PF $ 时，$ AP = $______.

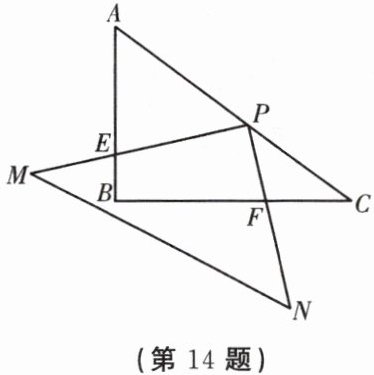
答案： 14.3

15. 如图，点 $ D $ 为矩形 $ OABC $ 的边 $ AB $ 的中点，反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图象经过点 $ D $，交 $ BC $ 边于点 $ E $. 若 $ \triangle BDE $ 的面积为 1，则 $ k = $______.

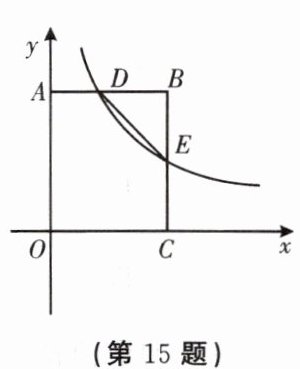
答案： 15.4

16. 过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形，如果其中一个是等腰三角形，另外一个三角形和原三角形相似，那么把这条线段定义为原三角形的“和谐分割线”. 如图，线段 $ CD $ 是 $ \triangle ABC $ 的“和谐分割线”，$ \triangle ACD $ 为等腰三角形，$ \triangle CBD $ 和 $ \triangle ABC $ 相似，$ \angle A = 46^{\circ} $，则 $ \angle ACB $ 的度数为______.

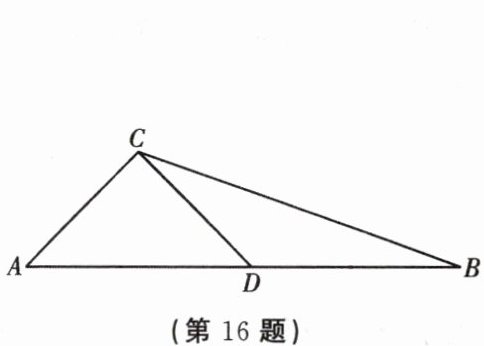
答案： 16.113°或92°