《2025年培优课堂七年级数学上册华师大版四川专版》

例题 对于有理数 $ a $、$ b $,定义 $ a \odot b = 2a - b $,则 $ (x + y) \odot (x - y) $ 化简后得 (D)
A.$ x - 3y $
B.$ x + y $
C.$ x - 2y $
D.$ x + 3y $

答案： D

1. 定义运算 $ a \bigstar b = |ab - 2a - b| $,如 $ 1 \bigstar 3 = |1×3 - 2×1 - 3| = 2 $。若 $ a = 2 $,且 $ a \bigstar b = 3 $,则 $ b $ 的值为 (D)
A.7
B.3
C.3 或 $ -3 $
D.1 或 7

答案： D

2. 用“☆”定义一种新运算：对于任意有理数 $ x $ 和 $ y $,$ x☆y = m^2x + ny - 3 $($ m $、$ n $ 为常数)。例如,$ 4☆3 = m^2·4 + n·3 - 3 = 4m^2 + 3n - 3 $。若 $ 2☆3 = 3 $,则 $ 4☆6 $ 的值为(C)
A.7
B.8
C.9
D.10

答案： C

3. 定义：有序有理数 $ a $、$ b $ 满足 $ a - b = ab + 1 $,则称有序有理数 $ a $、$ b $ 为“共生有序有理数”。若有序有理数 $ m $、$ n $ 是“共生有序有理数”,则下列各组有序有理数组合中,一定属于“共生有序有理数”的是 (D)
A.$ -m $,$ n $
B.$ m $,$ -n $
C.$ -m $,$ -n $
D.$ -n $,$ -m $

答案： D

4. 定义一种新运算：$ a※b = \begin{cases} a - b(a \geq b) \\ 3b(a ＜ b) \end{cases} $,则 $ 3※(-1)※5 $ 的结果是 (B)
A.$ -15 $
B.15
C.$ -1 $
D.$ -8 $

答案： B

5. 定义一种运算“※”：$ x※y = 2x - y - 1 $(其中 $ x $、$ y $ 为任意实数)。若当 $ a※b = 3 $ 时,则 $ (-5 + 2a)※2b $ 的值为 -3。

答案： -3

6. 十八世纪伟大的数学家欧拉最先用记号 $ f(x) $ 的形式来表示关于 $ x $ 的多项式,把 $ x $ 等于某数 $ n $ 时的多项式的值用 $ f(n) $ 来表示。例如,当 $ x = 1 $ 时,多项式 $ f(x) = 2x + 3 $ 的值可以记为 $ f(1) $,即 $ f(1) = 2×1 + 3 = 5 $。如果定义 $ f(x) = 3x^2 - 2x - 5 $,那么 $ f(2) = $ 3。

答案： 3

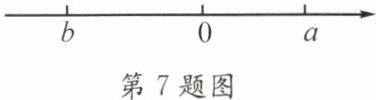
7. 对于有理数 $ a $、$ b $,定义一种新运算“&”,规定：$ a&b = |a| - |b| - |a - b| $。当 $ a $、$ b $ 在数轴上的位置如图所示时,化简 $ a&b = $ 2b。

答案： 2b

8. 定义一种新运算“$ \oplus $”：$ a \oplus b = 2a - 3b $。例如,$ 1 \oplus (-3) = 2×1 - 3×(-3) = 11 $。
(1) 求 $ (-2) \oplus 3 $ 的值；
(2) 若 $ A = (3x - 2) \oplus (x + 1) $,化简 $ A $。

答案：
(1)(-2)⊕3=2×(-2)-3×3=-4-9=-13.
(2)因为A=(3x-2)⊕(x+1),所以A=2(3x-2)-3(x+1)=6x-4-3x-3=3x-7.

9. 定义一种新运算“$ \odot $”,认真观察,寻找规律：
$ 1 \odot 3 = (-1) + 2×3 = 5 $；
$ (-5) \odot 4 = (+5) + 2×4 = 13 $；
$ 3 \odot (-1) = (-3) + 2×(-1) = -5 $；
$ (-2) \odot (-5) = (+2) + 2×(-5) = -8 $；
…
(1) 直接写出新定义的运算规律：$ a \odot b = $ -a+2b。
(2) 新运算“$ \odot $”是否满足交换律？请说明理由。
因为a⊙b=-a+2b,b⊙a=-b+2a,所以a⊙b-b⊙a=-a+2b-(-b+2a)=3b-3a.所以当a=b时,新运算“⊙”满足交换律;当a≠b时,新运算“⊙”不满足交换律.
(3) 先化简,再求值：$ (a - 3b) \odot (a - 2b) $,其中 $ a = 2 $,$ b = 2024 $。
(a-3b)⊙(a-2b)=3b-a+2(a-2b)=a-b.当a=2,b=2024时,原式=2-2024=-2022.

答案：
(1)-a+2b
(2)因为a⊙b=-a+2b,b⊙a=-b+2a,所以a⊙b-b⊙a=-a+2b-(-b+2a)=3b-3a.所以当a=b时,新运算“⊙”满足交换律;当a≠b时,新运算“⊙”不满足交换律.
(3)(a-3b)⊙(a-2b)=3b-a+2(a-2b)=a-b.当a=2,b=2024时,原式=2-2024=-2022.