第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
7. 【概念学习】
规定:求若干个相同的有理数(均不等于 $0$)的除法运算叫做除方,如 $2÷2÷2$,$(-3)÷(-3)÷(-3)÷(-3)$ 等。类比有理数的乘方,我们把 $2÷2÷2$ 记作 ,读作“$2$ 的圈 $3$ 次方”,$(-3)÷(-3)÷(-3)÷(-3)$ 记作
,读作“$2$ 的圈 $3$ 次方”,$(-3)÷(-3)÷(-3)÷(-3)$ 记作  ,读作“$-3$ 的圈 $4$ 次方”,一般地,把 $\underbrace{a÷ a÷…÷ a}_{n个a}(a\neq0)$ 记作 a^{\enclose{circle}{n}},读作“$a$ 的圈 $n$ 次方”。
,读作“$-3$ 的圈 $4$ 次方”,一般地,把 $\underbrace{a÷ a÷…÷ a}_{n个a}(a\neq0)$ 记作 a^{\enclose{circle}{n}},读作“$a$ 的圈 $n$ 次方”。
【初步探究】
(1) 直接写出计算结果: =
=  =
=
(2) 关于除方,下列说法错误的是
A. 任何非零数的圈 $2$ 次方都等于 $1$
B. 对于任何正整数 $n$,$1$ 的圈 $n$ 次方都等于 $1$
C.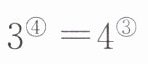
D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
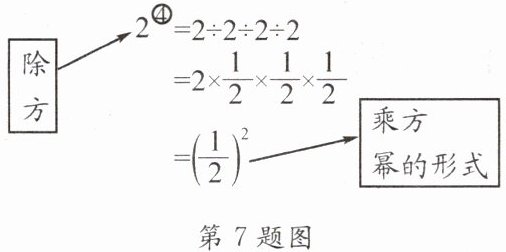
(3) 试一试:仿照上面的算式,将下列运算结果直接写成幂的形式。
$(-3)$ 的圈 $4$ 次方 =
(4) 想一想:将一个非零有理数 $a$ 的圈 $n$ 次方写成幂的形式为
(5) 算一算:24÷$2^{3}$ + (-8)× 。
。
规定:求若干个相同的有理数(均不等于 $0$)的除法运算叫做除方,如 $2÷2÷2$,$(-3)÷(-3)÷(-3)÷(-3)$ 等。类比有理数的乘方,我们把 $2÷2÷2$ 记作
 ,读作“$2$ 的圈 $3$ 次方”,$(-3)÷(-3)÷(-3)÷(-3)$ 记作
,读作“$2$ 的圈 $3$ 次方”,$(-3)÷(-3)÷(-3)÷(-3)$ 记作  ,读作“$-3$ 的圈 $4$ 次方”,一般地,把 $\underbrace{a÷ a÷…÷ a}_{n个a}(a\neq0)$ 记作 a^{\enclose{circle}{n}},读作“$a$ 的圈 $n$ 次方”。
,读作“$-3$ 的圈 $4$ 次方”,一般地,把 $\underbrace{a÷ a÷…÷ a}_{n个a}(a\neq0)$ 记作 a^{\enclose{circle}{n}},读作“$a$ 的圈 $n$ 次方”。【初步探究】
(1) 直接写出计算结果:
 =
= $\frac{1}{2}$
; =
= -8
。(2) 关于除方,下列说法错误的是
C
。A. 任何非零数的圈 $2$ 次方都等于 $1$
B. 对于任何正整数 $n$,$1$ 的圈 $n$ 次方都等于 $1$
C.
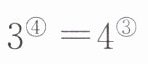
D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

(3) 试一试:仿照上面的算式,将下列运算结果直接写成幂的形式。
$(-3)$ 的圈 $4$ 次方 =
$\frac{1}{3^{2}}$
;$5$ 的圈 $5$ 次方 =$\frac{1}{5^{3}}$
;$(-\frac{1}{2})$ 的圈 $6$ 次方 =$2^{4}$
。(4) 想一想:将一个非零有理数 $a$ 的圈 $n$ 次方写成幂的形式为
$\frac{1}{a^{n-2}}$
。(5) 算一算:24÷$2^{3}$ + (-8)×
 。
。解:原式=$24÷8+(-8)×\frac{1}{2}=3-4=-1$
答案:
7.
(1)$\frac{1}{2}$ -8
(2)C
(3)$\frac{1}{3^{2}}$ $\frac{1}{5^{3}}$ $2^{4}$
(4)$\frac{1}{a^{n-2}}$
(5)解:原式=$24÷8+(-8)×\frac{1}{2}=3-4=-1$.
(1)$\frac{1}{2}$ -8
(2)C
(3)$\frac{1}{3^{2}}$ $\frac{1}{5^{3}}$ $2^{4}$
(4)$\frac{1}{a^{n-2}}$
(5)解:原式=$24÷8+(-8)×\frac{1}{2}=3-4=-1$.
8. 通过前面的学习我们知道:
$a^{2} = a\cdot a$,$a^{3} = a\cdot a\cdot a$,$a^{n} = a\cdot a…\cdot\cdot a$($n$ 个 $a$)。
(1) 探索发现:$(3×4)^{2} = $
你发现:$(3×4)^{2}$ 的值与 $3^{2}×4^{2}$ 的值
(2) 解决问题:利用(1)的结论尝试计算。
① $(-5)^{10}×(\frac{1}{5})^{10}$;
② $(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2024}×(4×3×2×1)^{2023}$。
①$(-5)^{10}×(\frac{1}{5})^{10}=(-5×\frac{1}{5})^{10}=1$.
②$(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2024}×(4×3×2×1)^{2023}$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2023}×(4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1×4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)=(-1)^{2023}×(-\frac{1}{24})=\frac{1}{24}$.
$a^{2} = a\cdot a$,$a^{3} = a\cdot a\cdot a$,$a^{n} = a\cdot a…\cdot\cdot a$($n$ 个 $a$)。
(1) 探索发现:$(3×4)^{2} = $
144
,$3^{2}×4^{2} = $144
;你发现:$(3×4)^{2}$ 的值与 $3^{2}×4^{2}$ 的值
相等
;猜想:$(a\cdot b)^{n}$=
$a^{n}\cdot b^{n}$。(2) 解决问题:利用(1)的结论尝试计算。
① $(-5)^{10}×(\frac{1}{5})^{10}$;
② $(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2024}×(4×3×2×1)^{2023}$。
①$(-5)^{10}×(\frac{1}{5})^{10}=(-5×\frac{1}{5})^{10}=1$.
②$(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2024}×(4×3×2×1)^{2023}$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2023}×(4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1×4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)=(-1)^{2023}×(-\frac{1}{24})=\frac{1}{24}$.
答案:
8.
(1)144 144 相等 =
(2)解:①$(-5)^{10}×(\frac{1}{5})^{10}=(-5×\frac{1}{5})^{10}=1$.
②$(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2024}×(4×3×2×1)^{2023}$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2023}×(4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1×4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)=(-1)^{2023}×(-\frac{1}{24})=\frac{1}{24}$.
(1)144 144 相等 =
(2)解:①$(-5)^{10}×(\frac{1}{5})^{10}=(-5×\frac{1}{5})^{10}=1$.
②$(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2024}×(4×3×2×1)^{2023}$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)^{2023}×(4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)$
$=(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1×4×3×2×1)^{2023}×(-\frac{1}{4}×\frac{1}{3}×\frac{1}{2}×1)=(-1)^{2023}×(-\frac{1}{24})=\frac{1}{24}$.
查看更多完整答案,请扫码查看


