第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
11. 我国出租车的收费标准因地而异。甲市为起步价 6 元,3 千米后每千米收费 $ 1.5 $ 元;乙市为起步价 10 元,3 千米后每千米收费 $ 1.2 $ 元。
(1)在甲、乙两市乘坐出租车行驶 $ x(x > 3) $ 千米的差价是多少元?
(2)如果在甲、乙两市乘坐出租车行驶的路程都为 10 千米,那么哪个城市的收费标准高一些?高多少?
(1)在甲、乙两市乘坐出租车行驶 $ x(x > 3) $ 千米的差价是多少元?
(2)如果在甲、乙两市乘坐出租车行驶的路程都为 10 千米,那么哪个城市的收费标准高一些?高多少?
答案:
解:
(1)在甲市乘坐出租车行驶$x(x>3)$千米的价格是$6+1.5(x-3)=(1.5x+1.5)$元,在乙市乘坐出租车行驶$x(x>3)$千米的价格是$10+1.2(x-3)=(1.2x+6.4)$元.所以在甲、乙两市乘坐出租车行驶$x(x>3)$千米的差价是$1.5x+1.5-1.2x-6.4=(0.3x-4.9)$元.
(2)当乘坐出租车行驶的路程为$10$千米时,在甲市收费为$1.5×10+1.5=16.5$(元),在乙市收费为$1.2×10+6.4=18.4$(元).因为$18.4>16.5$,$18.4-16.5=1.9$(元),所以在乙市的收费标准高一些,高$1.9$元.
(1)在甲市乘坐出租车行驶$x(x>3)$千米的价格是$6+1.5(x-3)=(1.5x+1.5)$元,在乙市乘坐出租车行驶$x(x>3)$千米的价格是$10+1.2(x-3)=(1.2x+6.4)$元.所以在甲、乙两市乘坐出租车行驶$x(x>3)$千米的差价是$1.5x+1.5-1.2x-6.4=(0.3x-4.9)$元.
(2)当乘坐出租车行驶的路程为$10$千米时,在甲市收费为$1.5×10+1.5=16.5$(元),在乙市收费为$1.2×10+6.4=18.4$(元).因为$18.4>16.5$,$18.4-16.5=1.9$(元),所以在乙市的收费标准高一些,高$1.9$元.
12. 某地电话拨号入网有两种收费方式,用户可以任选其一。A:计时制,$ 0.05 $ 元/分;B:包月制,50 元/月(限一部个人住宅电话上网)。此外,每一种上网方式都加收通信费 $ 0.02 $ 元/分。
(1)某用户每月上网时间为 $ x h $,请你分别写出两种收费方式下该用户应该支付的费用。
(2)若某用户估计一个月内上网的时间为 $ 20 h $,你认为采用哪种方式较为合算?
(1)某用户每月上网时间为 $ x h $,请你分别写出两种收费方式下该用户应该支付的费用。
(2)若某用户估计一个月内上网的时间为 $ 20 h $,你认为采用哪种方式较为合算?
答案:
解:
(1)根据题意,得计时制:$(0.05+0.02)×60x=4.2x$;包月制:$50+0.02×60x=50+1.2x$.
(2)当$x=20$时,计时制费用为$4.2×20=84$(元),包月制费用为$50+1.2×20=74$(元).因为$84>74$,所以当一个月内上网的时间为$20\ h$时,采用包月制较为合算.
(1)根据题意,得计时制:$(0.05+0.02)×60x=4.2x$;包月制:$50+0.02×60x=50+1.2x$.
(2)当$x=20$时,计时制费用为$4.2×20=84$(元),包月制费用为$50+1.2×20=74$(元).因为$84>74$,所以当一个月内上网的时间为$20\ h$时,采用包月制较为合算.
13. 甲仓库有水泥 $ 100 t $,乙仓库有水泥 $ 80 t $,要全部运到 A、B 两个工地,已知 A 工地需要 $ 70 t $,B 工地需要 $ 110 t $,甲仓库运到 A、B 两个工地的运费分别是 $ 140 $ 元/t、$ 150 $ 元/t,乙仓库运到 A、B 两个工地的运费分别是 $ 200 $ 元/t、$ 80 $ 元/t,本次运送水泥的总运费需要 $ 25900 $ 元。
(1)设甲仓库运到 A 工地水泥的吨数为 $ x $,请用含 $ x $ 的代数式填写下表(单位:t);
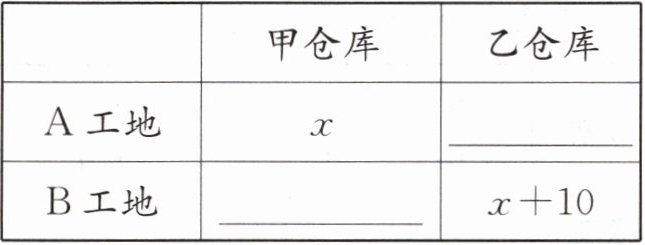
(2)用含 $ x $ 的代数式表示运送甲仓库 $ 100 t $ 水泥的运费为
(3)求出甲仓库运到 A 工地水泥的吨数。
(1)设甲仓库运到 A 工地水泥的吨数为 $ x $,请用含 $ x $ 的代数式填写下表(单位:t);

(2)用含 $ x $ 的代数式表示运送甲仓库 $ 100 t $ 水泥的运费为
$(-10x+15000)$
元;(写出化简后的结果)(3)求出甲仓库运到 A 工地水泥的吨数。
解:$140x+150(100-x)+200(70-x)+80(x+10)=25900$,整理,得$-130x+3900=0$,解得$x=30$.所以甲仓库运到A工地水泥的吨数是$30\ t$.
答案:
(1)$70-x$ $100-x$
(2)$(-10x+15000)$;
(3)解:$140x+150(100-x)+200(70-x)+80(x+10)=25900$,整理,得$-130x+3900=0$,解得$x=30$.所以甲仓库运到A工地水泥的吨数是$30\ t$.
(1)$70-x$ $100-x$
(2)$(-10x+15000)$;
(3)解:$140x+150(100-x)+200(70-x)+80(x+10)=25900$,整理,得$-130x+3900=0$,解得$x=30$.所以甲仓库运到A工地水泥的吨数是$30\ t$.
查看更多完整答案,请扫码查看


