第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 计算:
(1) $-(-3)^{3}=$
(2) $(-\frac{3}{4})^{2}=$
(3) $(-\frac{2}{3})^{3}=$
(4) $(-1\frac{2}{3})^{2}=$
(1) $-(-3)^{3}=$
27
;(2) $(-\frac{3}{4})^{2}=$
$\frac{9}{16}$
;(3) $(-\frac{2}{3})^{3}=$
$-\frac{8}{27}$
;(4) $(-1\frac{2}{3})^{2}=$
$\frac{25}{9}$
。
答案:
1.
(1)27
(2)$\frac{9}{16}$
(3)$-\frac{8}{27}$
(4)$\frac{25}{9}$
(1)27
(2)$\frac{9}{16}$
(3)$-\frac{8}{27}$
(4)$\frac{25}{9}$
2. 我们通常用到的数为十进制数,在表示十进制数时,我们需要用到 10 个数码:$0$,$1$,…,$9$,例如,$9810$,如果用我们刚学习过的乘方运算来表示,那么 $9810 = 9000 + 800 + 10 + 0 = 9×10^{3} + 8×10^{2} + 1×10^{1} + 0$。同样地,在表示三进制数时,我们需要用到 $3$ 个数码:$0$,$1$,$2$,例如,三进制数 $201 = 2×3^{2} + 0×3^{1} + 1$,等于十进制的数 $19$,那么二进制数 $10101$ 等于十进制的数
21
。
答案:
21
3. 观察下列算式:$3^{1} = 3$,$3^{2} = 9$,$3^{3} = 27$,$3^{4} = 81……$则 $3 + 3^{2} + 3^{3} + 3^{4} + 3^{5} + … + 3^{2024}$ 的末位数字是
0
。
答案:
0
$4. $类比有理数的乘方$,$我们把求若干个相同的有理数$($均不等于$ 0)$的除法运算叫做除方$,$记作  ,读作$“a $的圈$ n $次方$”。$如$ 2÷2÷2,$记作
,读作$“a $的圈$ n $次方$”。$如$ 2÷2÷2,$记作 ,读作$“2 $的圈$ 3 $次方$”;$$(-3)÷(-3)÷(-3)÷(-3) $记作
,读作$“2 $的圈$ 3 $次方$”;$$(-3)÷(-3)÷(-3)÷(-3) $记作  ,读作$“-3 $的圈$ 4 $次方$”,$除方也可以转化为幂的形式$,如 =$2÷2÷2÷2 = 2×\frac{1}{2}×\frac{1}{2}×\frac{1}{2} = (\frac{1}{2})^{2}$。 $
,读作$“-3 $的圈$ 4 $次方$”,$除方也可以转化为幂的形式$,如 =$2÷2÷2÷2 = 2×\frac{1}{2}×\frac{1}{2}×\frac{1}{2} = (\frac{1}{2})^{2}$。 $
(1) 计算: ; (2) 将一个非零有理数
; (2) 将一个非零有理数  写成幂的形式 (n\geq3)。$
写成幂的形式 (n\geq3)。$
 ,读作$“a $的圈$ n $次方$”。$如$ 2÷2÷2,$记作
,读作$“a $的圈$ n $次方$”。$如$ 2÷2÷2,$记作 ,读作$“2 $的圈$ 3 $次方$”;$$(-3)÷(-3)÷(-3)÷(-3) $记作
,读作$“2 $的圈$ 3 $次方$”;$$(-3)÷(-3)÷(-3)÷(-3) $记作  ,读作$“-3 $的圈$ 4 $次方$”,$除方也可以转化为幂的形式$,如 =$2÷2÷2÷2 = 2×\frac{1}{2}×\frac{1}{2}×\frac{1}{2} = (\frac{1}{2})^{2}$。 $
,读作$“-3 $的圈$ 4 $次方$”,$除方也可以转化为幂的形式$,如 =$2÷2÷2÷2 = 2×\frac{1}{2}×\frac{1}{2}×\frac{1}{2} = (\frac{1}{2})^{2}$。 $(1) 计算:
 ; (2) 将一个非零有理数
; (2) 将一个非零有理数  写成幂的形式 (n\geq3)。$
写成幂的形式 (n\geq3)。$
答案:
4.解:
(1) }=-2÷(-2)÷(-2)=-\frac{1}{2}.
}=-2÷(-2)÷(-2)=-\frac{1}{2}.
(2) =a÷ a÷\cdots÷ a=(\frac{1}{a})^{n-2}(n\geqslant3).
=a÷ a÷\cdots÷ a=(\frac{1}{a})^{n-2}(n\geqslant3).
n个
4.解:
(1)
 }=-2÷(-2)÷(-2)=-\frac{1}{2}.
}=-2÷(-2)÷(-2)=-\frac{1}{2}.(2)
 =a÷ a÷\cdots÷ a=(\frac{1}{a})^{n-2}(n\geqslant3).
=a÷ a÷\cdots÷ a=(\frac{1}{a})^{n-2}(n\geqslant3).n个
5. 细菌繁殖时,一个细菌分裂成两个,一个细菌在分裂 $n$ 次后,数量变为 $2^{n}$ 个。有一种细菌,它的分裂速度很快,每 $12$ min 分裂一次,如果现在盘子里有 $1000$ 个这样的细菌,那么 $60$ min 后,盘子里有多少个细菌?$2$ h 后细菌的个数是 $1$ h 后的多少倍?
答案:
5.解:$60÷12=5$(次),
所以60 min后,盘子里有细菌:$1000×2^{5}=32000$(个).
2 h=120 min,$120÷12=10$(次),
所以2 h后,盘子里有$(1000×2^{10})$个细菌.
$1000×2^{10}÷(1000×2^{5})=2^{5}=32$,
故60 min后,盘子里有32000个细菌,2 h后细菌的个数是1 h后的32倍.
所以60 min后,盘子里有细菌:$1000×2^{5}=32000$(个).
2 h=120 min,$120÷12=10$(次),
所以2 h后,盘子里有$(1000×2^{10})$个细菌.
$1000×2^{10}÷(1000×2^{5})=2^{5}=32$,
故60 min后,盘子里有32000个细菌,2 h后细菌的个数是1 h后的32倍.
6. “数形结合”是一种重要的数学思想,观察下面的图形和算式。
$1 + 3 = 4 = 2^{2}$;
$1 + 3 + 5 = 9 = 3^{2}$;
$1 + 3 + 5 + 7 = 16 = 4^{2}$;
$1 + 3 + 5 + 7 + 9 = 25 = 5^{2}$。
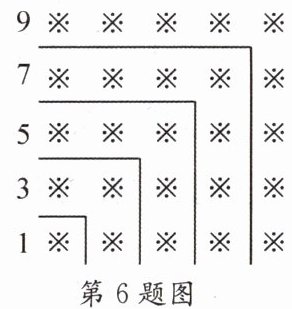
解答下列问题:
(1) $1 + 3 + 5 + 7 + 9 + … + 19 = $
(2) 当 $n$ 是正整数时,$1 + 3 + 5 + 7 + 9 + 11 + … + (2n - 1) = $
(3) 请用(2)中得到的规律计算:$19 + 21 + 23 + 25 + 27 + … + 99$。
$1 + 3 = 4 = 2^{2}$;
$1 + 3 + 5 = 9 = 3^{2}$;
$1 + 3 + 5 + 7 = 16 = 4^{2}$;
$1 + 3 + 5 + 7 + 9 = 25 = 5^{2}$。

解答下列问题:
(1) $1 + 3 + 5 + 7 + 9 + … + 19 = $
100
$=$(____10
)$^{2}$;(2) 当 $n$ 是正整数时,$1 + 3 + 5 + 7 + 9 + 11 + … + (2n - 1) = $
$n^{2}$
;(3) 请用(2)中得到的规律计算:$19 + 21 + 23 + 25 + 27 + … + 99$。
答案:
6.
(1)100 10
(2)$n^{2}$
(3)解:$19+21+23+25+27+\cdots+99$
$=(1+3+5+\cdots+99)-(1+3+5+7+\cdots+17)$
$=50^{2}-9^{2}=2419$.
(1)100 10
(2)$n^{2}$
(3)解:$19+21+23+25+27+\cdots+99$
$=(1+3+5+\cdots+99)-(1+3+5+7+\cdots+17)$
$=50^{2}-9^{2}=2419$.
查看更多完整答案,请扫码查看


