第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
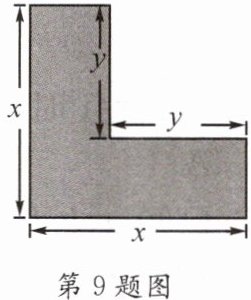
9. (1)请用含$x和y$的代数式来表示阴影部分的面积.
(2)当$x = 4$,$y = 3$时,阴影部分的面积是多少?
(2)当$x = 4$,$y = 3$时,阴影部分的面积是多少?

答案:
(1)依题意,阴影部分的面积等于大正方形的面积减去小正方形的面积,即阴影部分的面积等于$x^{2}-y^{2}$.
(2)当x=4,y=3时,$x^{2}-y^{2}=16-9=7$.
(1)依题意,阴影部分的面积等于大正方形的面积减去小正方形的面积,即阴影部分的面积等于$x^{2}-y^{2}$.
(2)当x=4,y=3时,$x^{2}-y^{2}=16-9=7$.
10. 按下图所示的程序计算,若开始输入的$x的值是- 2$,则最后输出的结果是 (
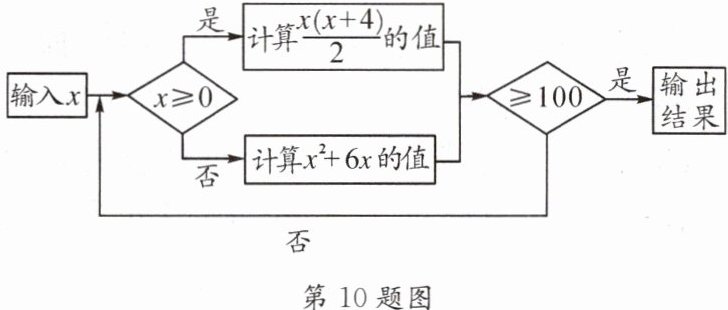
A.$150$
B.$160$
C.$170$
D.$180$
B
)
A.$150$
B.$160$
C.$170$
D.$180$
答案:
B
11. 甲、乙两家超市为了促销同一种定价相同的商品,甲超市连续两次降价$10\%$,乙超市一次性降价$20\%$,那么顾客购买哪家超市的商品更合算一些 (
A.甲
B.乙
C.同样
D.无法确定
B
)A.甲
B.乙
C.同样
D.无法确定
答案:
B
12. 若当$x = 1$时,代数式$- 2px^{3} + 3qx + 1的值是2024$,则当$x = - 1$时,代数式$- 2px^{3} + 3qx + 1$的值是
-2022
.
答案:
-2022
13. 某服装厂生产一种西装和领带,西装每套定价$200$元,领带每条定价$40$元. 厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的$90\%$付款.
现某客户要到该服装厂购买西装$20$套,领带$x条(x > 20)$.
(1)若该客户按方案①购买,需付款
(2)若$x = 30$,通过计算说明此时按哪种方案购买较为合算?
①买一套西装送一条领带;
②西装和领带都按定价的$90\%$付款.
现某客户要到该服装厂购买西装$20$套,领带$x条(x > 20)$.
(1)若该客户按方案①购买,需付款
(40x+3200)
元(用含$x$的代数式表示,下同);若该客户按方案②购买,需付款(3600+36x)
元.(2)若$x = 30$,通过计算说明此时按哪种方案购买较为合算?
解:当x=30时,按方案①购买,需付款$40x+3200=$40×30+3200=4400(元);按方案②购买,需付款$3600+36x=3600+36×30=4680$(元).因为4400<4680,所以选择方案①购买较为合算.
答案:
(1)(40x+3200) (3600+36x)
(2)解:当x=30时,按方案①购买,需付款$40x+3200=$40×30+3200=4400(元);按方案②购买,需付款$3600+36x=3600+36×30=4680$(元).因为4400<4680,所以选择方案①购买较为合算.
(1)(40x+3200) (3600+36x)
(2)解:当x=30时,按方案①购买,需付款$40x+3200=$40×30+3200=4400(元);按方案②购买,需付款$3600+36x=3600+36×30=4680$(元).因为4400<4680,所以选择方案①购买较为合算.
14. (1)当$a = 5$,$b = 3$时,分别求代数式$(a - b)^{2}与a^{2} - 2ab + b^{2}$的值.
(2)当$a = - 4$,$b = 2$时,分别求代数式$(a - b)^{2}与a^{2} - 2ab + b^{2}$的值.
(3)从(1)(2)中你发现了什么规律?利用你的发现,求当$a = \frac{2022}{2023}$,$b = - \frac{2024}{2023}$时,代数式$a^{2} - 2ab + b^{2}$的值.
(2)当$a = - 4$,$b = 2$时,分别求代数式$(a - b)^{2}与a^{2} - 2ab + b^{2}$的值.
(3)从(1)(2)中你发现了什么规律?利用你的发现,求当$a = \frac{2022}{2023}$,$b = - \frac{2024}{2023}$时,代数式$a^{2} - 2ab + b^{2}$的值.
答案:
(1)当a=5,b=3时,$(a-b)^{2}=(5-3)^{2}=4$;$a^{2}-2ab+b^{2}=5^{2}-2×5×3+3^{2}=4$.
(2)当a=-4,b=2时,$(a-b)^{2}=(-4-2)^{2}=36$;$a^{2}-2ab+b^{2}=(-4)^{2}-2×(-4)×2+2^{2}=36$.
(3)从
(1)
(2)中可发现:$a^{2}-2ab+b^{2}=(a-b)^{2}$.当a=$\frac{2022}{2023}$,b=-$\frac{2024}{2023}$时,代数式$a^{2}-2ab+b^{2}=(a-b)^{2}=(\frac{2022}{2023}+\frac{2024}{2023})^{2}=2^{2}=4$.
(1)当a=5,b=3时,$(a-b)^{2}=(5-3)^{2}=4$;$a^{2}-2ab+b^{2}=5^{2}-2×5×3+3^{2}=4$.
(2)当a=-4,b=2时,$(a-b)^{2}=(-4-2)^{2}=36$;$a^{2}-2ab+b^{2}=(-4)^{2}-2×(-4)×2+2^{2}=36$.
(3)从
(1)
(2)中可发现:$a^{2}-2ab+b^{2}=(a-b)^{2}$.当a=$\frac{2022}{2023}$,b=-$\frac{2024}{2023}$时,代数式$a^{2}-2ab+b^{2}=(a-b)^{2}=(\frac{2022}{2023}+\frac{2024}{2023})^{2}=2^{2}=4$.
15. 对于正整数$a$,我们规定:若$a$为奇数,则$f(a) = 3a + 1$;若$a$为偶数,则$f(a) = \frac{a}{2}$.
例如,$f(9) = 3×9 + 1 = 28$,$f(10) = \frac{10}{2} = 5$. 若$a_{1} = 8$,$a_{2} = f(a_{1})$,$a_{3} = f(a_{2})$,$a_{4} = f(a_{3})……$依此规律进行下去,得到一列数$a_{1}$,$a_{2}$,$a_{3}$,…,$a_{n}$($n$为正整数),则$a_{3} = $
例如,$f(9) = 3×9 + 1 = 28$,$f(10) = \frac{10}{2} = 5$. 若$a_{1} = 8$,$a_{2} = f(a_{1})$,$a_{3} = f(a_{2})$,$a_{4} = f(a_{3})……$依此规律进行下去,得到一列数$a_{1}$,$a_{2}$,$a_{3}$,…,$a_{n}$($n$为正整数),则$a_{3} = $
2
;$a_{1} + a_{2} + a_{3} + … + a_{2024} = $4730
.
答案:
2 4730
查看更多完整答案,请扫码查看


