第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 圆是由
曲线
围成的封闭图形. 在同一平面内,由一些不在同一直线上的线段首尾顺次
连结所组成的封闭图形
叫做多边形. 按组成多边形的边数
,多边形可分为三角形、四边形、五边形、六边形……
答案:
曲线 首尾顺次 封闭图形 边数
2. $n$边形从一个顶点出发,可以引
$(n-3)$
条对角线;$n$边形总的对角线条数是$\frac{n(n-3)}{2}$
条.
答案:
$(n-3)$ $\frac{n(n-3)}{2}$
3. 三角形是最简单的多边形,所有的多边形都可看作是由
过$n$边形的一顶点,连结不相邻的顶点,可将多边形分割成
过$n$边形一边上的任意一点(顶点除外),连结不相邻的顶点,可将多边形分割成
过$n$边形内任意一点,连结多边形各个顶点,可将多边形分割成
三角形
组成的,任意一个多边形都可分割成若干个三角形. 分法不同,分得的三角形的个数也不同. 例如:过$n$边形的一顶点,连结不相邻的顶点,可将多边形分割成
$(n-2)$
个三角形.过$n$边形一边上的任意一点(顶点除外),连结不相邻的顶点,可将多边形分割成
$(n-1)$
个三角形.过$n$边形内任意一点,连结多边形各个顶点,可将多边形分割成
$n$
个三角形.
答案:
三角形 $(n-2)$ $(n-1)$ $n$
例1 有下列图形:①三角形;②长方形;③平行四边形;④立方体;⑤圆锥;⑥圆柱;⑦圆;⑧球体. 其中属于平面图形的有(
A.5种
B.4种
C.3种
D.2种
B
)A.5种
B.4种
C.3种
D.2种
答案:
B
例2 【观察思考】如图,五边形$ABCDE$内部有若干个点,用这些点以及五边形$ABCDE的顶点A$、$B$、$C$、$D$、$E$把原五边形分割成一些三角形(互相不重叠).
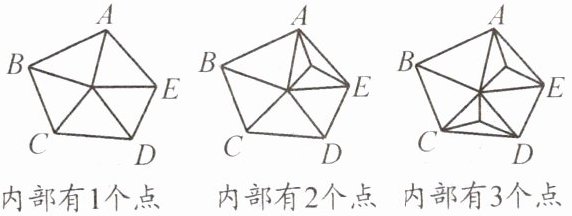
【规律总结】
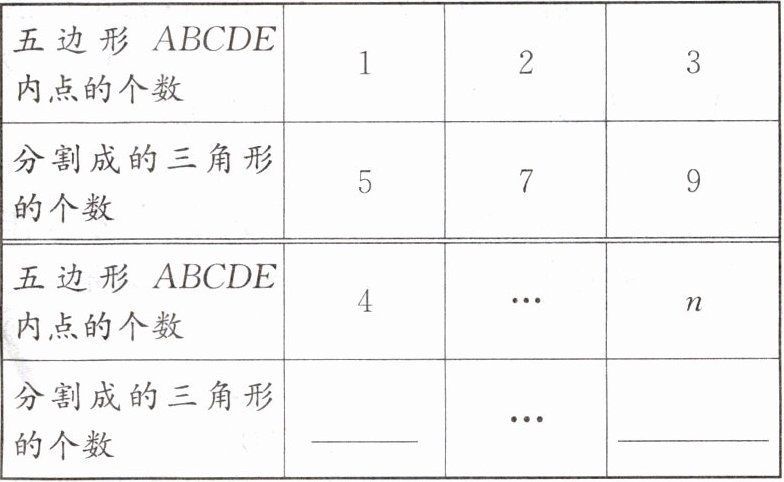
【问题解决】
(2)原五边形能否被分割成2023个三角形?若能,求出此时五边形$ABCDE$的内部有多少个点;若不能,请说明理由.

【规律总结】

【问题解决】
(2)原五边形能否被分割成2023个三角形?若能,求出此时五边形$ABCDE$的内部有多少个点;若不能,请说明理由.
解:原五边形能被分割成2023个三角形.
由题意,得$2n+3=2023$,解得$n=1010$,且符合实际.
所以原五边形能被分割成2023个三角形,内部有1010个点.
由题意,得$2n+3=2023$,解得$n=1010$,且符合实际.
所以原五边形能被分割成2023个三角形,内部有1010个点.
答案:
(1)11 $2n+3$
(2)解:原五边形能被分割成2023个三角形.
由题意,得$2n+3=2023$,解得$n=1010$,且符合实际.
所以原五边形能被分割成2023个三角形,内部有1010个点.
(1)11 $2n+3$
(2)解:原五边形能被分割成2023个三角形.
由题意,得$2n+3=2023$,解得$n=1010$,且符合实际.
所以原五边形能被分割成2023个三角形,内部有1010个点.
1. 下面四个几何图形中,表示平面图形的是(
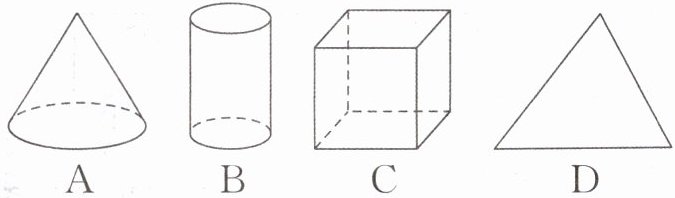
D
)
答案:
D
2. 下列说法正确的是(
A.由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形
B.一条弧和经过弧的两条半径所围成的图形叫做扇形
C.三角形是最简单的多边形
D.圆的一部分是扇形
C
)A.由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形
B.一条弧和经过弧的两条半径所围成的图形叫做扇形
C.三角形是最简单的多边形
D.圆的一部分是扇形
答案:
C
3. 下图中甲和乙的周长相比,结果是(
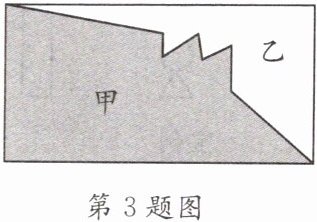
A.甲比乙长
B.甲比乙短
C.甲和乙一样长
D.无法比较
C
)
A.甲比乙长
B.甲比乙短
C.甲和乙一样长
D.无法比较
答案:
C
查看更多完整答案,请扫码查看


