《2025年培优课堂七年级数学上册华师大版四川专版》

7. 下列事实可以用“经过两点有且只有一条直线”来说明的是 (B)
A.从王庄到李庄走直线最近
B.在正常情况下,射击时要保证瞄准的一只眼睛在准星和缺口确定的直线上,才能射中目标
C.向远方延伸的铁路给我们一条直线的印象
D.数轴是一条特殊的直线

答案： B

8. 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是两点确定一条直线.

答案： 两点确定一条直线

9. 如图,图中共有6条线段,5条射线,0条直线.

答案： 6 5 0

10. 如图,已知A、B、C、D四点,按下列语句画出图形：
(1)画直线AB；
(2)画射线AD；
(3)连结AC、BD,交于点O.

答案：
解:如图所示.

11. 如图,以A、B、C、D、E为端点的线段共有 (B)

A.8条
B.10条
C.12条
D.14条

答案： B

12. 过平面内一点画直线,可以画无数条；过平面内两点画直线,可以画1条；过平面内三点中任意两点画直线,可以画1或3条；过平面内四点中任意两点画直线,可以画1或4或6条.

答案： 无数 1 1或3 1或4或6

13. 某市长途客运有几条线路承包给个体司机,从该市(图中的点O)出发,跑长途的有三条线路：①号线、②号线和③号线. 这三条线路分别通往不同的区县,点$ A $、$ B_1 $、$ B_2 $、$ C_1 $、$ C_2 $、$ C_3 $分别代表车站,承包人必须印制多少种车票,才能便于正常运营？

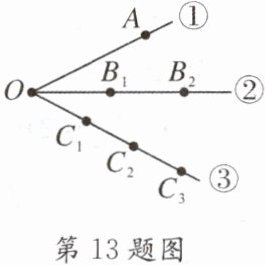
答案： 解:①号线有1条线段，有1种票价;②号线有3条线段,有3种票价;③号线有6条线段,有6种票价,共有1+3+6=10(种)票价,另外还需出售返程车票，所以承包人必须印制20种车票，才能便于正常运营.

14. 如图.

(1)试验观察：
如果每过两点可以画一条直线,那么：
第①组最多可以画3条直线；
第②组最多可以画6条直线；
第③组最多可以画10条直线.
(2)探索归纳：
如果平面上有$ n ( n \geqslant 3 ) $个点,且每3个点均不在一条直线上,那么最多可以画$\frac{n(n−1)}{2}$条直线.(用含$ n $的代数式表示)
(3)解决问题：
某班有45名同学,在毕业后的一次聚会中,若每两人握1次手问好,则共握990次手.

答案：
(1)3 6 10
(2)$\frac{n(n−1)}{2}$
(3)990