《2025年培优课堂七年级数学上册华师大版四川专版》

6. 【信息提取】
在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如,$|6+7|= 6+7$,$|6-7|= 7-6$,$|7-6|= 7-6$,$|-6-7|= 6+7$.
【初步体验】
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式(不要计算出结果)：
①$|7-21|=$21-7；
②$|\frac{7}{17}-\frac{7}{18}|=$$\frac{7}{17}-\frac{7}{18}$.
【拓展应用】
(2)计算：
$|\frac{1}{3}-\frac{1}{2}|+|\frac{1}{4}-\frac{1}{3}|+|\frac{1}{5}-\frac{1}{4}|+…+|\frac{1}{2021}-\frac{1}{2020}|+|\frac{1}{2022}-\frac{1}{2021}|+|\frac{1}{2023}-\frac{1}{2022}|+|\frac{1}{2024}-\frac{1}{2023}|$.
解:原式$=\frac{1011}{2024}$.

答案： 6.
(1)①$21-7$ ②$\frac{7}{17}-\frac{7}{18}$
(2)解:原式$=\frac{1011}{2024}$.

7. 某汽车厂计划半年内每月生产汽车$20$辆,由于另有任务,每月上班人数不一定相等,实际每月生产量与计划量相比情况如下表(增加为正,减少为负)：

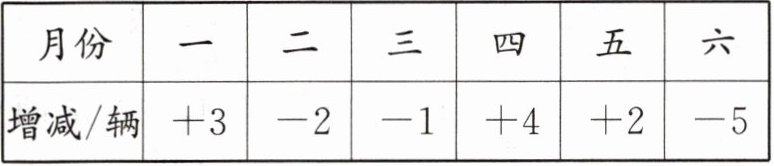
(1)生产量最多的月份比生产量最少的月份多生产多少辆？
(2)半年内生产的总量是多少？比计划多了还是少了,多或少了多少？

答案： 7.解:
(1)由表格可知,生产量最多的月份为四月份,共生产了$20+4=24$(辆);
生产量最少的月份为六月份,共生产了$20-5=15$(辆).
所以生产量最多的月份比生产量最少的月份多生产$24-15=9$(辆).
(2)半年内生产的总量为$(3-2-1+4+2-5)+20× 6=121$(辆);
计划每月生产20辆,则半年共生产$20× 6=120$(辆).
因为$121-120=1$(辆),所以半年内生产的总量为121辆,比计划多了,多了1辆.