第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
12. 求$ 2^{1} + 2^{2} + 2^{3} + 2^{4} + … + 2^{99} + 2^{100} $的值,直接计算较困难,因为$ 2^{100} $是一个非常大的数.因此,我们用解方程的方法来求解.
解:设$ x = 2^{1} + 2^{2} + 2^{3} + 2^{4} + … + 2^{99} + 2^{100} $.①
所以$ 2x = 2 × (2^{1} + 2^{2} + 2^{3} + 2^{4} + … + 2^{99} + 2^{100}) $,
即$ 2x = 2^{2} + 2^{3} + 2^{4} + … + 2^{100} + 2^{101} $.②
② - ①,得$ 2x - x = 2^{2} + 2^{3} + 2^{4} + … + 2^{100} + 2^{101} - (2^{1} + 2^{2} + 2^{3} + 2^{4} + … + 2^{99} + 2^{100}) $
$ = 2^{101} - 2 $.
所以原式$ = 2^{101} - 2 $.
请你在理解的基础上,模仿上述方法求下列各式的值:
(1)$ 2^{101} - 2^{1} - 2^{2} - 2^{3} - 2^{4} - … - 2^{99} - 2^{100} = $
(2)$ 1 + 3^{1} + 3^{2} + 3^{3} + 3^{4} + … + 3^{2023} + 3^{2024} $.
解:设$ x = 2^{1} + 2^{2} + 2^{3} + 2^{4} + … + 2^{99} + 2^{100} $.①
所以$ 2x = 2 × (2^{1} + 2^{2} + 2^{3} + 2^{4} + … + 2^{99} + 2^{100}) $,
即$ 2x = 2^{2} + 2^{3} + 2^{4} + … + 2^{100} + 2^{101} $.②
② - ①,得$ 2x - x = 2^{2} + 2^{3} + 2^{4} + … + 2^{100} + 2^{101} - (2^{1} + 2^{2} + 2^{3} + 2^{4} + … + 2^{99} + 2^{100}) $
$ = 2^{101} - 2 $.
所以原式$ = 2^{101} - 2 $.
请你在理解的基础上,模仿上述方法求下列各式的值:
(1)$ 2^{101} - 2^{1} - 2^{2} - 2^{3} - 2^{4} - … - 2^{99} - 2^{100} = $
2
;(2)$ 1 + 3^{1} + 3^{2} + 3^{3} + 3^{4} + … + 3^{2023} + 3^{2024} $.
解:设y=1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴①
所以3y=3×(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴),
即3y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵.②
②-①,得3y-y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵-(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴)=3²⁰²⁵-1.
所以2y=3²⁰²⁵-1.所以原式=$\frac{3^{2025}-1}{2}$.
所以3y=3×(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴),
即3y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵.②
②-①,得3y-y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵-(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴)=3²⁰²⁵-1.
所以2y=3²⁰²⁵-1.所以原式=$\frac{3^{2025}-1}{2}$.
答案:
(1)2
(2)解:设y=1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴①
所以3y=3×(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴),
即3y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵.②
②-①,得3y-y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵-(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴)=3²⁰²⁵-1.
所以2y=3²⁰²⁵-1.所以原式=$\frac{3^{2025}-1}{2}$.
(1)2
(2)解:设y=1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴①
所以3y=3×(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴),
即3y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵.②
②-①,得3y-y=3+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴+3²⁰²⁵-(1+3¹+3²+3³+3⁴+…+3²⁰²³+3²⁰²⁴)=3²⁰²⁵-1.
所以2y=3²⁰²⁵-1.所以原式=$\frac{3^{2025}-1}{2}$.
13. 如图所示,体育课上,小明的实心球成绩为9.6m,则他投出的实心球落在(
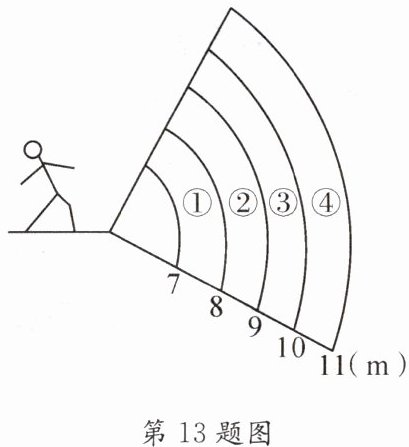
A.区域①
B.区域②
C.区域③
D.区域④
C
)
A.区域①
B.区域②
C.区域③
D.区域④
答案:
C
14. 近似数$ 3.14 × 10^{3} $精确到(
A.百分位
B.个位
C.十位
D.百位
C
)A.百分位
B.个位
C.十位
D.百位
答案:
C
15. 截至2月底,全国电影票房累计约3300000000元.数据3300000000用科学记数法表示为(
A.$ 33 × 10^{8} $
B.$ 3.3 × 10^{8} $
C.$ 3.3 × 10^{9} $
D.$ 3.3 × 10^{10} $
C
)A.$ 33 × 10^{8} $
B.$ 3.3 × 10^{8} $
C.$ 3.3 × 10^{9} $
D.$ 3.3 × 10^{10} $
答案:
C
查看更多完整答案,请扫码查看


