《2025年培优课堂七年级数学上册华师大版四川专版》

8. 某产粮专业户出售余粮 $20$ 袋,每袋质量(单位：kg)如下：199,201,197,203,200,195,197,199,202,196,203,198,201,200,197,196,204,199,201,198。用简便方法计算出售的余粮总共多少千克。

答案： 解:设每袋余粮的标准质量为200 kg,超出的记为正,不足的记为负,这20袋余粮的质量可记为-1,+1,-3,+3,0,-5,-3,-1,+2,-4,+3,-2,+1,0,-3,-4,+4,-1,+1,-2.这20个数的和为-14,所以这20袋余粮的总质量为200×20-14=3986(kg).答:出售的余粮总共3986 kg.

9. 某水利勘察队,第一天向上游走了 $5\frac{1}{2}$ km,第二天向下游走了 $5\frac{1}{3}$ km,第三天向上游走了 $4\frac{2}{3}$ km,第四天向下游走了 $5\frac{1}{2}$ km,这时勘察队在出发点(D)
A.上游 $1\frac{1}{3}$ km 处
B.下游 $1$ km 处
C.上游 $\frac{2}{3}$ km 处
D.下游 $\frac{2}{3}$ km 处

答案： D

10. 去年7月份小明到银行开户,存入 $1500$ 元钱,以后每月的存取情况如下表所示(正的代表存入,负的代表支出)：

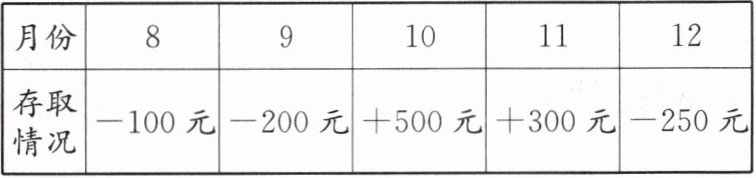
截至去年12月份,存折上共有1750元。

答案： 1750

11. 计算：
(1)$0.75+(-2\frac{3}{4})+(+0.125)+(-12\frac{5}{7})+(-4\frac{1}{8})$；
(2)$3\frac{7}{12}+(-1\frac{1}{4})+(-3\frac{7}{12})+1\frac{1}{4}+(-4\frac{1}{8})$。

答案： $(1)$计算$0.75+(-2\frac{3}{4})+(+0.125)+(-12\frac{5}{7})+(-4\frac{1}{8})$
解：
将小数化为分数：$0.75 = \frac{3}{4}$，$0.125=\frac{1}{8}$
$\begin{aligned}&0.75+(-2\frac{3}{4})+(+0.125)+(-12\frac{5}{7})+(-4\frac{1}{8})\\=&\frac{3}{4}-2\frac{3}{4}+\frac{1}{8}-12\frac{5}{7}-4\frac{1}{8}\\=&(\frac{3}{4}-2\frac{3}{4})+(\frac{1}{8}-4\frac{1}{8})-12\frac{5}{7}\\=&(\frac{3}{4}-\frac{11}{4})+(\frac{1}{8}-\frac{33}{8})-12\frac{5}{7}\\=&\frac{3 - 11}{4}+\frac{1 - 33}{8}-12\frac{5}{7}\\=&-\frac{8}{4}-\frac{32}{8}-12\frac{5}{7}\\=& - 2-4-12\frac{5}{7}\\=&-6 - 12\frac{5}{7}\\=&-18\frac{5}{7}\end{aligned}$
$(2)$计算$3\frac{7}{12}+(-1\frac{1}{4})+(-3\frac{7}{12})+1\frac{1}{4}+(-4\frac{1}{8})$
解：
$\begin{aligned}&3\frac{7}{12}+(-1\frac{1}{4})+(-3\frac{7}{12})+1\frac{1}{4}+(-4\frac{1}{8})\\=&(3\frac{7}{12}-3\frac{7}{12})+(1\frac{1}{4}-1\frac{1}{4})-4\frac{1}{8}\\=&0 + 0-4\frac{1}{8}\\=&-4\frac{1}{8}\end{aligned}$
综上，$(1)$的结果是$-18\frac{5}{7}$；$(2)$的结果是$-4\frac{1}{8}$。

12. 探究规律,回答相关问题。
小明说：“我在有理数内定义了一种新的运算,叫 $*$(加乘)运算。”然后他写出了一些按照 $*$(加乘)运算的运算法则进行运算的算式：
$(+5)*(+2)= +7$；
$(-3)*(-5)= +8$；
$(-3)*(+4)= -7$；
$(+5)*(-6)= -11$；
$0*(+8)= 8$；$(-6)*0= 6$。
(1)归纳 $*$(加乘)运算的运算法则：
两数进行 $*$(加乘)运算时,同号得正、异号得负,并把绝对值相加；
特别地,0和任何数进行 $*$(加乘)运算,或任何数和0进行 $*$(加乘)运算,都得这个数的绝对值。
(2)计算：$(-2)*[0*(-1)]=$-3。(括号的作用与有理数运算中的作用一致)
(3)我们知道加法有交换律和结合律,这两种运算律在有理数的 $*$(加乘)运算中还适用吗？请你任选一个运算律,判断它在 $*$(加乘)运算中是否适用,并举例验证。(举一个例子即可)
解:加法的交换律仍然适用.举例:$(-3)*(-5)=8$,$(-5)*(-3)=8$,所以$(-3)*(-5)=(-5)*(-3)$.故加法的交换律仍然适用.加法的结合律不适用.举例:$[(-3)*(-4)]*0=7$,$(-3)*[(-4)*0]=-7$,所以$[(-3)*(-4)]*0≠(-3)*[(-4)*0]$.故加法的结合律不适用.

答案：
(1)同号得正、异号得负,并把绝对值相加 都得这个数的绝对值
(2)-3
(3)解:加法的交换律仍然适用.举例:$(-3)*(-5)=8$,$(-5)*(-3)=8$,所以$(-3)*(-5)=(-5)*(-3)$.故加法的交换律仍然适用.加法的结合律不适用.举例:$[(-3)*(-4)]*0=7$,$(-3)*[(-4)*0]=-7$,所以$[(-3)*(-4)]*0≠(-3)*[(-4)*0]$.故加法的结合律不适用.