第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
7. 观察下列各式:
$1^{2}+1 = 1×2$;$2^{2}+2 = 2×3$;$3^{2}+3 = 3×4$……
请你将猜想的规律用自然数$n(n≥1)$表示出来:
$1^{2}+1 = 1×2$;$2^{2}+2 = 2×3$;$3^{2}+3 = 3×4$……
请你将猜想的规律用自然数$n(n≥1)$表示出来:
$n^{2}+n=n(n+1)$
。
答案:
$n^{2}+n=n(n+1)$
8. 同学们,你们还记得“青蛙绕口令”吗?
|一只青蛙一张嘴,两只眼睛四条腿,扑通一声跳下水。两只青蛙两张嘴,四只眼睛八条腿,扑通两声跳下水。|
若有a只青蛙,则用绕口令怎么说?请你用今天所学的知识解决这个问题。
|一只青蛙一张嘴,两只眼睛四条腿,扑通一声跳下水。两只青蛙两张嘴,四只眼睛八条腿,扑通两声跳下水。|
若有a只青蛙,则用绕口令怎么说?请你用今天所学的知识解决这个问题。
答案:
解:由于青蛙的嘴数、跳下水的声音数和只数一样,眼睛数是只数的2倍,腿数是只数的4倍,所以当有$a$只青蛙时,青蛙的嘴数是$a$张,眼睛数是$2a$只,腿数是$4a$条.故绕口令为“$a$只青蛙$a$张嘴,$2a$只眼睛$4a$条腿,扑通$a$声跳下水.”
9. 用字母表示图中阴影部分的面积。


答案:
解:图1:$ab-bx$;图2:$R^{2}-\frac{1}{4}\pi R^{2}$.
10. 正方形的边长为a cm,边长增加2cm后,面积增加(
A.$4cm^{2}$
B.$(a^{2}+4)cm^{2}$
C.$[(a + 2)^{2}+a^{2}]cm^{2}$
D.$[(a + 2)^{2}-a^{2}]cm^{2}$
D
)A.$4cm^{2}$
B.$(a^{2}+4)cm^{2}$
C.$[(a + 2)^{2}+a^{2}]cm^{2}$
D.$[(a + 2)^{2}-a^{2}]cm^{2}$
答案:
D
11. 小明从一排座位的第m个开始数,一直数到第n个$(n>m)$,他数过的座位数是(
A.$(m + n)$个
B.$(n - m)$个
C.$(n - m - 1)$个
D.$(n - m + 1)$个
D
)A.$(m + n)$个
B.$(n - m)$个
C.$(n - m - 1)$个
D.$(n - m + 1)$个
答案:
D
12. 如图1是一个三角形,分别连结这个三角形三边的中点,得到图2,再连结图2中间小三角形三边的中点,得到图3,按这样的方法进行下去,第n个图形中三角形的个数为(
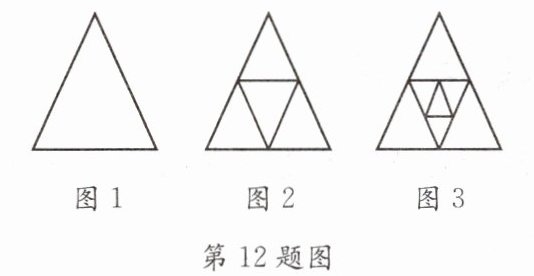
A.$2n - 3$
B.$4n - 1$
C.$4n - 3$
D.$4n - 2$
C
)
A.$2n - 3$
B.$4n - 1$
C.$4n - 3$
D.$4n - 2$
答案:
C
13. 如图,数轴上O、A两点间的距离为4,一动点P从点A出发,第1次跳动到AO的中点$A_{1}$处,第2次从点$A_{1}跳动到A_{1}O的中点A_{2}$处,第3次从点$A_{2}跳动到A_{2}O的中点A_{3}$处,按照这样的规律继续跳动到点$A_{4}$、$A_{5}$、$A_{6}$、…、$A_{n}$处,那么线段$A_{n}A$的长度为
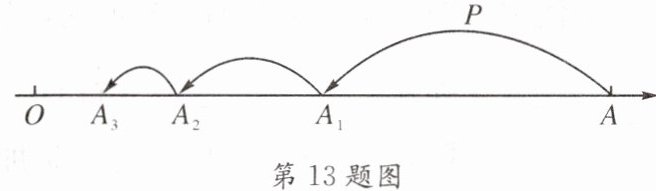
$4-(\frac{1}{2})^{n}×4$
。
答案:
$4-(\frac{1}{2})^{n}×4$
14. 【观察思考】如图是某同学在棋盘上用围棋子摆成的图案。
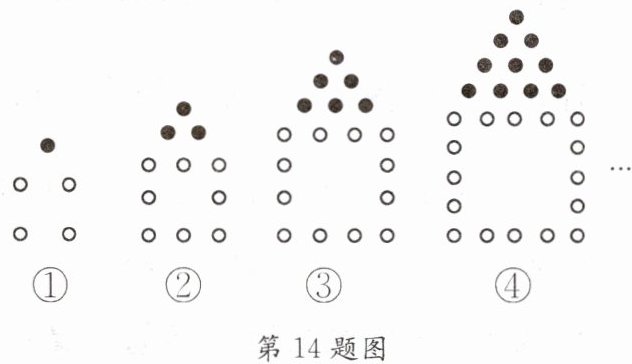
【规律发现】
(1)第⑤个图案中“●”的枚数为
(2)第n个图案中“●”的枚数为
【规律应用】
(3)该同学准备用100枚“●”棋子和100枚“○”棋子摆放第n个图案,摆放成完整的图案后,n的最大值为

【规律发现】
(1)第⑤个图案中“●”的枚数为
15
,“○”的枚数为20
;(2)第n个图案中“●”的枚数为
$\frac{n(n+1)}{2}$
,“○”的枚数为$4n$
;【规律应用】
(3)该同学准备用100枚“●”棋子和100枚“○”棋子摆放第n个图案,摆放成完整的图案后,n的最大值为
13
;此时还剩下57
枚棋子。
答案:
(1)15 20
(2)$\frac{n(n+1)}{2}$ $4n$
(3)13 57
(1)15 20
(2)$\frac{n(n+1)}{2}$ $4n$
(3)13 57
查看更多完整答案,请扫码查看


