《2025年考出好成绩八年级数学上册青岛版山东专版》

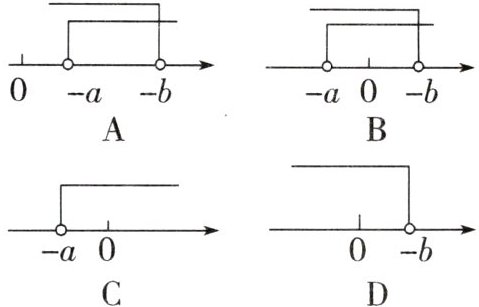
11. 把不等式组$\begin{cases}x ＞ -a, \\ x ＜ -b\end{cases} (b ＜ a ＜ 0)$的解集表示在数轴上,正确的是 (A)

答案： A

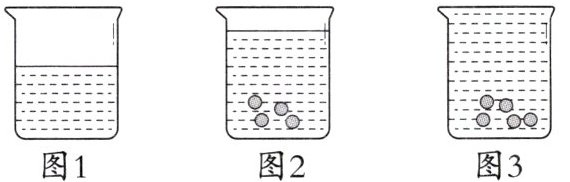
12. (2025 潍坊期末)测量一种玻璃球的体积,小亮的方法是:①将$500\ cm^3的水倒进一个容量为700\ cm^3$的杯子中;②将四颗相同的玻璃球放人水中,结果水没有满;③再将一颗同样大小的玻璃球放入水中,结果水满溢出. 根据这个现象,小亮判断这样的一个玻璃球的体积可能是 (C)

A.$35\ cm^3$
B.$40\ cm^3$
C.$45\ cm^3$
D.$50\ cm^3$

答案： C

13. 解不等式组:
(1) $\begin{cases}2(x - 1) \leqslant 5x + 4,① \\ 3(x + 4) ＞ 2(2x + 1);②\end{cases} $
(2) $\begin{cases}2(x + 2) - x \leqslant 5,① \\ \dfrac{4x + 1}{3} ＞ x - 1.②\end{cases} $

答案： 解:
(1)解不等式①,得$x\geqslant -2.$解不等式②,得$x＜10.$
∴该不等式组的解集为$-2\leqslant x＜10.$
(2)解不等式①,得$x\leqslant 1.$解不等式②,得$x＞-4.$
∴该不等式组的解集为$-4＜x\leqslant 1.$

14. 已知$a是不等式组\begin{cases}5a - 1 ＞ 3(a + 1), \\ \dfrac{1}{2}a - 1 ＜ 7 - \dfrac{3}{2}a\end{cases} $的整数解,$x,y满足方程组\begin{cases}ax - 2y = 8, \\ x + 2y = 0,\end{cases} 求(x - y)(x^{2} + xy + y^{2})$的值.

答案： 解:解不等式$5a-1＞3(a+1)$,得$a＞2.$解不等式$\frac{1}{2}-1＜7-\frac{3}{2}a$,得$a＜4.$
∴该不等式组的解集是$2＜a＜4.$
∵a是整数,
∴$a=3.$
∴$\left\{\begin{array}{l} 3x-2y=8,\\ x+2y=0,\end{array}\right. $解得$\left\{\begin{array}{l} x=2,\\ y=-1,\end{array}\right. $$\therefore (x-y)(x^{2}+xy+y^{2})=(2+1)(4-2+1)=3×3=9.$

15. 已知关于$x,y的方程组\begin{cases}x + 2y = 1, \\ x - y = m.\end{cases} $
(1) 求这个方程组的解;
(2) 当$m$取何值时,这个方程组的解中,$x大于1$,$y不小于-1$.

答案： 解:
(1)$\left\{\begin{array}{l} x+2y=1,①\\ x-y=m,②\end{array}\right. $①-②,得$3y=1-m$,则$y=\frac{1-m}{3}.$①+2×②,得$3x=1+2m$,则$x=\frac{1+2m}{3}.$
∴这个方程组的解为$\left\{\begin{array}{l} x=\frac{1+2m}{3},\\ y=\frac{1-m}{3}.\end{array}\right. $
(2)根据题意,得$\left\{\begin{array}{l} \frac{2m+1}{3}＞1,\\ \frac{1-m}{3}\geqslant -1,\end{array}\right. $解得$1＜m\leqslant 4.$