第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
11.已知$\triangle ABC内接于\odot O$,$AB= AC$,$O到BC$的距离为6,$\odot O$的半径为10,则$AB$的长为
$4\sqrt{5}$或$8\sqrt{5}$
.
答案:
$4\sqrt{5}$或$8\sqrt{5}$
12.(2024·武昌)我国明代科学家徐光启在《农政全书》中描绘了一种我国古代常用的水利灌溉工具——筒车,如图,筒车盛水桶的运行轨道是以轴心$O$为圆心的圆,已知圆心$O$在水面的上方,$\odot O被水面截得的弦AB$长为6米,点$C$是运动轨道的最低点.点$C$到水面的距离为2米,则$\odot O$的半径长为(

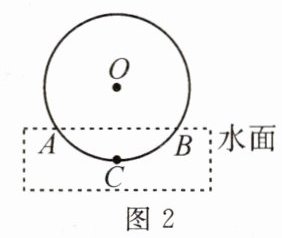
A.$\frac{13}{4}$米
B.5米
C.4米
D.$\frac{11}{4}$米
A
)

A.$\frac{13}{4}$米
B.5米
C.4米
D.$\frac{11}{4}$米
答案:
A
13.(教材P89T8改编)如图,在$\odot O$中,直径$AB⊥弦CD$,$E$为垂足,$AE= 4$,$CE= 6$,求$\odot O$的半径为
$\frac{13}{2}$
.
答案:
解:连接OC,设$\odot O$半径为R,$6^{2}+(R-4)^{2}=R^{2}$,$R=\frac{13}{2}$.
14.(教材P90T12变式)如图,某地有一座圆弧形拱桥,桥下水面宽度$AB$为7.2m,拱高$CD$为2.4m.
(1)求拱桥的半径$R$;
(2)现有一艘宽3m、船舱顶部为长方形并高出水面2m的货船要经过这里,此货船能顺利通过拱桥吗?
(1)求拱桥的半径$R$;
3.9m
(2)现有一艘宽3m、船舱顶部为长方形并高出水面2m的货船要经过这里,此货船能顺利通过拱桥吗?
能
答案:
(1)连接OA,$R=3.9m$.
(2)在AB上取$DE=DF=1.5m$,
作$EM⊥AB$,$FN⊥AB$,分别交$\overset{\frown}{AB}$于M,N,连接MN交OC于H,连接ON,
在$Rt\triangle OHN$中可求$OH=3.6$,
$\because OD=1.5$,$\therefore DH=2.1$,
$\therefore NF>2$,$\therefore$能通过.
(1)连接OA,$R=3.9m$.
(2)在AB上取$DE=DF=1.5m$,
作$EM⊥AB$,$FN⊥AB$,分别交$\overset{\frown}{AB}$于M,N,连接MN交OC于H,连接ON,
在$Rt\triangle OHN$中可求$OH=3.6$,
$\because OD=1.5$,$\therefore DH=2.1$,
$\therefore NF>2$,$\therefore$能通过.
15.(教材P90T10改编)在半径为5的$\odot O$中,弦$AB= 6$,弦$CD= 8$,且$AB// CD$,则$AB与CD$之间的距离为
7或1
.
答案:
7或1
查看更多完整答案,请扫码查看


