《2025年思维新观察九年级数学上册人教版》

7.某村计划建造如图所示的矩形蔬菜温室,要求温室的长宽之比为2:1,在温室内,距前侧内墙保留3m宽的空地,其他三个侧墙内各保留1m宽的通道,蔬菜种植区域的面积是$288m^2$时,矩形温室长为多少(B)
A.14
B.28
C.20
D.30

答案： B

8.(2025·河南)手卷是国画装裱中横幅的一种体式,以能握在手中顺序展开阅览得名,它主要由“引首”“画心”“拖尾”三部分组成(这三部分都是矩形),分隔这三部分的其余部分统称为“隔水”.图中手卷长1000cm,宽40cm,引首和拖尾完全相同,其宽度都为100cm,若画心的面积为$15200cm^2,$求隔水的宽度x.

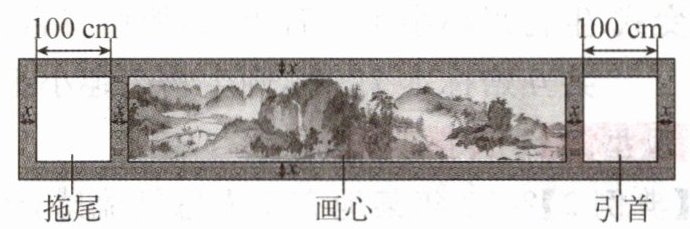
隔水的宽度x为10cm。

答案： 解: 已知隔水的宽度为$xcm$，则画心的长为$(1000 - 2×100 - 4x)cm$，宽为$(40 - 2x)cm$。
根据题意, 得$(1000 - 2×100 - 4x)(40 - 2x) = 15200$，
解得$x = 10$或$x = 210$(舍去)，
$\therefore$隔水的宽度$x$为 10 cm。

9.(2024·广东)社区利用一块矩形空地ABCD建了一个小型停车场,其布局如图所示.已知AD= 52m,AB= 28m,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为x米的道路,已知铺花砖的面积为$640m^2.$
(1)求道路的宽是多少米?
答: 道路的宽为6米。
(2)该停车场共有车位50个,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为10125元?
答: 当每个车位的月租金上涨25元时, 停车场的月租金收入为10125元。

答案： 解:
(1) 根据题意得，
$(52 - 2x)(28 - 2x) = 640$，
整理得:$x^{2} - 40x + 204 = 0$，
解得:$x_{1} = 34$(舍去)，$x_{2} = 6$。
答: 道路的宽为 6 米。
(2) 设月租金上涨$a$元, 停车场月租金收入为 10125 元，
根据题意得:$(200 + a)(50 - \frac{a}{5}) = 10125$，整理得:$a^{2} - 50a + 625 = 0$，解得$a = 25$。
答: 当每个车位的月租金上涨 25 元时, 停车场的月租金收入为 10125 元。