《2025年思维新观察九年级数学上册人教版》

5.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式是:$h= 30t-5t^{2}(0≤t≤6)$,则小球从第1s到第5s的运动路径长为(40m)
A.20m
B.30m
C.40m
D.50m

答案： C
解: $ t = 1 $，$ h = 25 $；$ t = 3 $，$ h = 45 $；
$ t = 5 $，$ h = 25 $. 故路径长为 40m.

6.(教材P51探究3变式)如图是抛物线形的拱桥,当拱顶离水面2m时,水面宽4m.
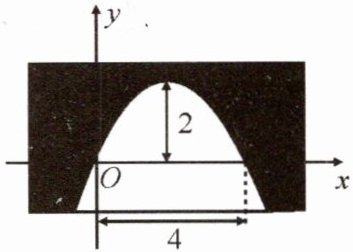
(1)建立如图所示的平面直角坐标系,求抛物线的解析式;$ y = -\frac{1}{2}(x - 2)^{2} + 2 $
(2)如果水面宽为$2\sqrt {6}m$,则水面下降多少米?1m

答案： 解:
(1) $ \because $ 抛物线的顶点坐标为 $ (2, 2) $，可设抛物线的解析式为 $ y = a(x - 2)^{2} + 2 $，点 $ (4, 0) $ 在抛物线上，可得 $ 0 = a(4 - 2)^{2} + 2(a \neq 0) $，解得 $ a = -\frac{1}{2} $.
$ \therefore y = -\frac{1}{2}(x - 2)^{2} + 2 $.
(2) 1m.

7.(2024·黄石)如图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.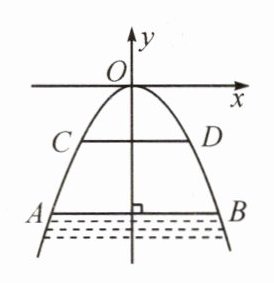
(1)在如图的坐标系中求抛物线的解析式;$ y = -\frac{1}{25}x^{2} $
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?5

答案： 解:
(1) 设抛物线的解析式 $ y = ax^{2} $，
$ D(5, b) $，$ B(10, b - 3) $，
$ \begin{cases} 25a = b \\ 100a = b - 3 \end{cases} $，$ \therefore \begin{cases} a = -\frac{1}{25} \\ b = -1 \end{cases} $，$ \therefore y = -\frac{1}{25}x^{2} $；
(2) $ t = \frac{1}{0.2} = 5 $ (小时).

8.如图,队员甲正在投篮,已知球出手时离地面高$\frac {20}{9}$米,与篮筐中心的水平距离为7米,当球出手后水平距离4米时,到达最大高度为4米,设篮球运行的轨迹是抛物线,篮筐距地面为3米.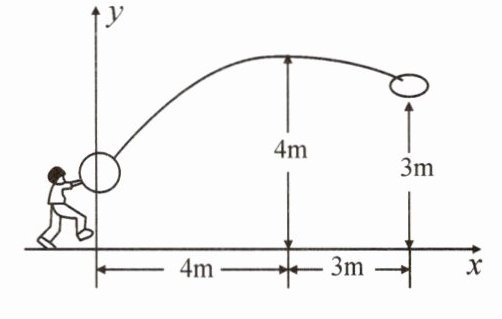
(1)建立如图所示的平面直角坐标系,此球能否准确投中?能投中
(2)此时,若对方队员乙在甲前方1米处跳起盖帽拦截,已知乙的最大摸高为3.1米,那么他盖帽能成功吗?能成功

答案： 解:
(1) 设解析式为 $ y = a(x - 4)^{2} + 4(a \neq 0) $，
$ \therefore \frac{20}{9} = a(0 - 4)^{2} + 4 $，
$ \therefore a = -\frac{1}{9} $，
$ \therefore y = -\frac{1}{9}x^{2} + \frac{8}{9}x + \frac{20}{9} $，
当 $ x = 7 $ 时，$ y = 3 $，能投中.
(2) 当 $ x = 1 $ 时，$ y = 3 $，$ 3 ＜ 3.1 $，能成功.