《2025年思维新观察九年级数学上册人教版》

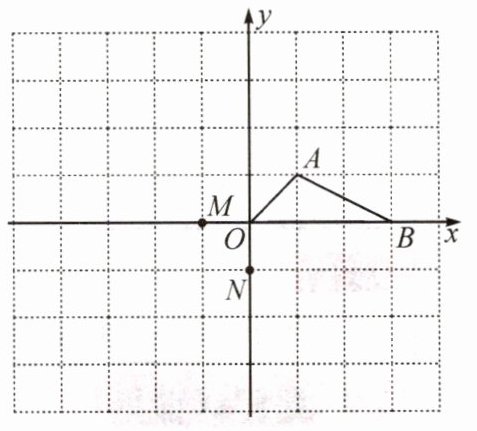
6.如图,在平面直角坐标系中有A(1,1),B(3,0)两点.
(1)画出$△ABO$关于M(-1,0)成中心对称的$△A_{1}B_{1}O_{1}$,直接写出A1(______);
(2)将$△ABO$绕点N(0,-1)顺时针旋转90°得$△A_{2}B_{2}O_{2}$,画出$△A_{2}B_{2}O_{2}$,并写出A点经过的路径长为______.

答案：

(1)如图所示,$(-3,-1)$;
(2)如图所示,$\frac {\sqrt {5}}{2}π$

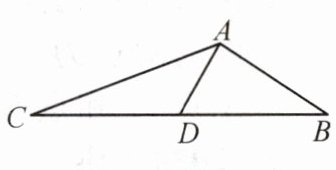
7.(2024·武汉)如图,在$△ABC$中,D为BC的中点.
(1)用圆规和无刻度直尺画出$△ABD$关于点D的对称图形;
(2)若AC= 4,AB= 2,$∠CAB= 120^{\circ}$,求AD的长.

答案：
解:
(1)如图所示;

(2)由中心对称的性质知,$△CDE\cong △BDA,CE// AB,∠ACE=60^{\circ },$
过E点作$EF⊥AC$于F点,$CF=1,EF=\sqrt {3},$
$\therefore AE=2\sqrt {3},\therefore AD=\sqrt {3}.$

8.(2025·湖北)综合探究:在$△ABC$中,$∠ACB= 90^{\circ}$,把$△ABC$绕点A逆时针旋转β($0^{\circ}＜β＜180^{\circ}$)得到$△ADE$,点B的对应点为点D,点C的对应点为点E.
(1)如图1,若BC交AD于点O,延长线交DE于点P.求证:PC= PE;
证明:连接AP,$Rt△ACP\cong △Rt△AEP,\therefore CP=PE$
(2)如图2,延长EC交BD于点M,判断M是否为线段BD的中点,并说明理由;
过点B作$BH// DE$交EM的延长线于点H,设$∠BCM=\alpha,\therefore ∠MED=∠BHC=\alpha,\therefore BH=BC=DE,\therefore △BHM\cong △DEM,\therefore BM=DM$
(3)如图3,EC与BD,AD分别交于点M,N,当DA⊥AC,$\frac{AC}{BC}= \frac{3}{4}$时,若BD= 2$\sqrt{10}$,求CN的长.
$\frac {2}{3}\sqrt {10}$

答案：
(1)证明:连接AP,
$Rt△ACP\cong △Rt△AEP,\therefore CP=PE;$
(2)过点B作$BH// DE$交EM的延长线于点H,
设$∠BCM=\alpha,\therefore ∠MED=∠BHC=\alpha,$
$\therefore BH=BC=DE,$
$\therefore △BHM\cong △DEM,\therefore BM=DM;$
(3)连接AM,设$AC=3x$,则$BC=4x$,
由
(2)知$BM=DM,\therefore △BCM\cong △DNM,$
$\therefore DN=4x,\therefore AM=\frac {1}{2}CN=\frac {1}{2}\sqrt {10}x,$
在$Rt△ABM$中,
$(\frac {1}{2}\sqrt {10}x)^{2}+(\sqrt {10})^{2}=(5x)^{2},x=\frac {2}{3},$
$\therefore CN=\frac {2}{3}\sqrt {10}.$