第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
1.如图,在长为100米、宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644平方米,则道路的宽应为多少米?设道路的宽为x米,则可列方程为
(100 - x)(80 - x) = 7644
.
答案:
$(100 - x)(80 - x) = 7644$
2.如图所示,在宽为20m,长为32m的矩形地面上修筑相同宽度的甬道(图中阴影部分),余下部分种上草坪,要使草坪面积为$540m^2,$设甬道宽为x m,可列方程为
$(32 - x)(20 - x) = 540$
.
答案:
$(32 - x)(20 - x) = 540$
3.如图,矩形绿地ABCD的长AB为42m,宽BC为30m,灰色区域为宽度相等的一条“7”形的健身用鹅卵石小路,若鹅卵石小路的面积为$140m^2,$则小路的宽BE为(
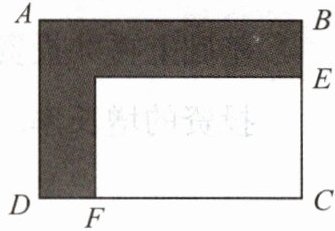
A.1m
B.1.5m
C.2m
D.2.5m
2m
)
A.1m
B.1.5m
C.2m
D.2.5m
答案:
C
解: 设$BE = xm$,
则$(30 - x)(42 - x) = 42×30 - 140$,
$x_{1} = 2$,$x_{2} = 70$(舍),
$\therefore BE = 2m$。
解: 设$BE = xm$,
则$(30 - x)(42 - x) = 42×30 - 140$,
$x_{1} = 2$,$x_{2} = 70$(舍),
$\therefore BE = 2m$。
4.如图,用48米的篱笆在一个长为25米的墙边靠墙围成一个面积为300平方米的长方形鸡场,鸡场有一个宽为2米的门,求鸡场的长与宽.
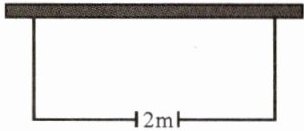
解: 设垂直于墙的一边长为

解: 设垂直于墙的一边长为
x
米, 则长为(50 - 2x)
米, 其中0 <50 - 2x ≤ 25,$\frac{25}{2}$
≤ x < 25,根据题意, 可列方程为$x(50 - 2x) = 300$
,解得$x_{1} = $15
,$x_{2} = $10
(舍去)。$\therefore$长为20
米, 宽为15
米。
答案:
解: 设垂直于墙的一边长为$x$米, 则长为$(50 - 2x)$米, 其中$0 <$
$50 - 2x \leq 25$,$\frac{25}{2} \leq x < 25$,根据题意, 可列方程为$x(50 - 2x) = 300$,
解得$x_{1} = 15$,$x_{2} = 10$(舍去)。
$\therefore$长为 20 米, 宽为 15 米。
$50 - 2x \leq 25$,$\frac{25}{2} \leq x < 25$,根据题意, 可列方程为$x(50 - 2x) = 300$,
解得$x_{1} = 15$,$x_{2} = 10$(舍去)。
$\therefore$长为 20 米, 宽为 15 米。
5.(教材P20探究3变式)要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的$\frac{17}{81},$上、下边衬等宽,左、右边衬等宽,求上、下边衬的宽.
答案:
解: 设中央的矩形的长为$9xcm$,宽为$7xcm$,
则$9x \cdot 7x = \frac{64}{81}×27×21$,
$x_{1} = \frac{8}{3}$,$x_{2} = -\frac{8}{3}$(舍),
故上、下边衬宽为$(27 - \frac{8}{3}×9)×\frac{1}{2} = \frac{3}{2}cm$。
则$9x \cdot 7x = \frac{64}{81}×27×21$,
$x_{1} = \frac{8}{3}$,$x_{2} = -\frac{8}{3}$(舍),
故上、下边衬宽为$(27 - \frac{8}{3}×9)×\frac{1}{2} = \frac{3}{2}cm$。
6.武汉云雾山景区有一块$8×5m^2$的矩形郁金香园地,现在其中修建一条观花道(阴影部分)供游人赏花,若改造后观花道面积为$12m^2,$求x的值.
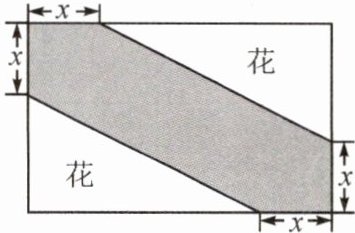
解:$8×5 - (8 - x)(5 - x) = 12$,
$\therefore x^{2} - 13x + 12 = 0$,$\therefore x_{1} = 12$,$x_{2} = 1$,$\because x \leq 5$,$\therefore x = $

解:$8×5 - (8 - x)(5 - x) = 12$,
$\therefore x^{2} - 13x + 12 = 0$,$\therefore x_{1} = 12$,$x_{2} = 1$,$\because x \leq 5$,$\therefore x = $
1
。
答案:
解:$8×5 - (8 - x)(5 - x) = 12$,
$\therefore x^{2} - 13x + 12 = 0$,$\therefore x_{1} = 12$,$x_{2} = 1$,$\because x \leq 5$,$\therefore x = 1$。
$\therefore x^{2} - 13x + 12 = 0$,$\therefore x_{1} = 12$,$x_{2} = 1$,$\because x \leq 5$,$\therefore x = 1$。
查看更多完整答案,请扫码查看


