《2025年思维新观察九年级数学上册人教版》

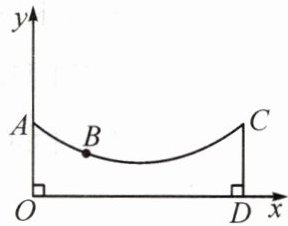
【典例】(2024·荆门)为装饰墙面,在墙面上的点A,C分别钉一颗钉子,在A,C之间悬挂一条近似抛物线的彩带.$AO⊥OD,CD⊥OD,AO= CD$,以水平地面上OD所在直线为x轴,OA所在直线为y轴,建立如图所示的平面直角坐标系,抛物线的解析式为$y= 0.1x^{2}-0.8x+3$.
(1)求OD的长;8
(2)现要在抛物线上的点B处粘贴一个气球(不改变抛物线的形状),已知点B到CD的距离为6m,求点B到水平地面OD的距离.1.8m

答案： 解:
(1)抛物线解析式 $ y = 0.1x^{2} - 0.8x + 3 $ 化为顶点式为 $ y = 0.1(x - 4)^{2} + 1.4 $，
∴抛物线的顶点坐标为 $ (4,1.4) $，
∵ $ AO \perp OD $，$ CD \perp OD $，$ AO = CD $，
∴ $ A $，$ C $ 关于对称轴 $ x = 4 $ 对称，
∴ $ OD = 8 $；
(2)
∵点 $ B $ 到 $ CD $ 的距离为 $ 6m $，
∴点 $ B $ 到 $ OA $ 的距离为 $ 2m $，
∴ $ y_{B} = 0.1 \times 2^{2} - 0.8 \times 2 + 3 = 1.8m $．
答:点 $ B $ 到水平地面 $ OD $ 的距离为 $ 1.8m $．

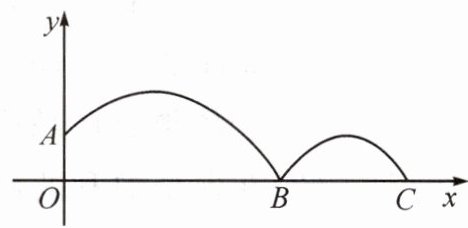
变式.(2024·黄石)如图,小明站在原点处,从高地面高度为1m的点A处抛出弹力球,弹力球在B处着地后弹起,落至点C处,弹力球着地前后的运动轨迹可近似看成形状相同的两条抛物线,弹力球第一次着地前抛物线的解析式为$y= a(x-2)^{2}+2$,弹力球在B处着地后弹起的最大高度为着地前手抛出的最大高度的一半,如果在地上摆放一个底面半径为0.5m,高为0.5m的圆柱形筐,筐的最左端距离原点为n米,若要弹力球从B点弹起后落入筐内,则n的值可以是(B)
A.7
B.8
C.9
D.10

答案： B
解:第一次抛物线 $ y = -\frac{1}{4}(x - 2)^{2} + 2 $，
$ B(2 + 2\sqrt{2},0) $；
第二次抛物线 $ y = -\frac{1}{4}(x - 2\sqrt{2} - 4)^{2} + 1 $，
∴ $ C(2\sqrt{2} + 6,0) $，$ OC = 2\sqrt{2} + 6 $，
当 $ y = 0.5 $ 时，
$ -\frac{1}{4}(x - 2\sqrt{2} - 4)^{2} + 1 = \frac{1}{2} $，
$ x_{1} = 4 + 3\sqrt{2} $，$ x_{2} = 4 + \sqrt{2} $，
$ 3 + 3\sqrt{2} \leq n \leq 4 + 3\sqrt{2} $，故 $ n $ 可以是 $ 8 $．