第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
【典例】(2023·武汉)中山公园的人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安装一个喷水头,喷出的水柱形状可看作是抛物线的一部分.若记水柱上某一点的位置与水管的水平距离为x米,与湖面的垂直高度为y米,表中记录了x与y的五组数据:

(1)根据表中所给数据,在图1建立的平面直角坐标系中画出表示y与x函数关系的图象;
(2)求y与x的函数表达式;
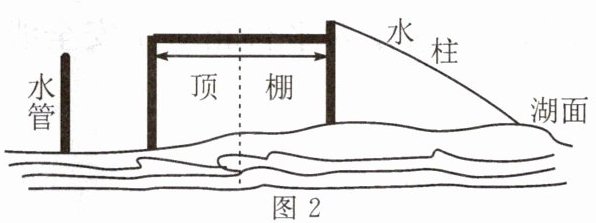
(3)公园准备调节水管露出湖面的高度,使游船能从抛物线形水柱下方通过.如图2所示,为避免游船被喷泉淋到,要求游船以抛物线的对称轴为中轴线从水柱下方通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米.已知游船顶棚宽度为2米,顶棚到湖面的高度为1.8米,请计算分析水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?
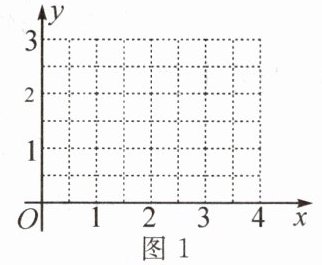

(1)根据表中所给数据,在图1建立的平面直角坐标系中画出表示y与x函数关系的图象;
(2)求y与x的函数表达式;
(3)公园准备调节水管露出湖面的高度,使游船能从抛物线形水柱下方通过.如图2所示,为避免游船被喷泉淋到,要求游船以抛物线的对称轴为中轴线从水柱下方通过时,顶棚上任意一点到水柱的竖直距离均不小于0.5米.已知游船顶棚宽度为2米,顶棚到湖面的高度为1.8米,请计算分析水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求?


答案:
【典例】解:
(1)如图1所示;
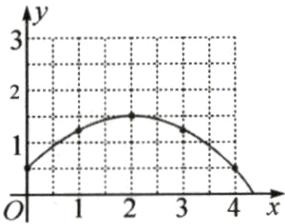
(2)表中数据$(1,1.25),(3,1.25)$,由抛物线的轴对称性可知:该抛物线的顶点坐标为$(2,1.5)$.
设二次函数的解析式为$y=a(x-2)^{2}+1.5(a≠0)$,
将$(0,0.5)$代入$y=a(x-2)^{2}+1.5$,解得$a=-\frac {1}{4}$,
∴抛物线的解析式为$y=-\frac {1}{4}(x-2)^{2}+1.5$,
即$y=-\frac {1}{4}x^{2}+x+0.5$;
(3)设水管高度至少上调h米.
∴调节后的水管喷出的抛物线的解析式为$y=-\frac {1}{4}x^{2}+x+0.5+h$,由题意可知:当横坐标为$2-1=1$或$2+1=3$时,纵坐标的值不小于$1.8+0.5=2.3$,
$\therefore -\frac {1}{4}×3^{2}+3+0.5+h≥2.3$,解得$h≥1.05$,
∴水管高度至少向上调节1.05米,
$1.05+0.5=1.55$(米),
∴水管露出湖面的高度至少调节到约1.55米才能符合要求.
【典例】解:
(1)如图1所示;

(2)表中数据$(1,1.25),(3,1.25)$,由抛物线的轴对称性可知:该抛物线的顶点坐标为$(2,1.5)$.
设二次函数的解析式为$y=a(x-2)^{2}+1.5(a≠0)$,
将$(0,0.5)$代入$y=a(x-2)^{2}+1.5$,解得$a=-\frac {1}{4}$,
∴抛物线的解析式为$y=-\frac {1}{4}(x-2)^{2}+1.5$,
即$y=-\frac {1}{4}x^{2}+x+0.5$;
(3)设水管高度至少上调h米.
∴调节后的水管喷出的抛物线的解析式为$y=-\frac {1}{4}x^{2}+x+0.5+h$,由题意可知:当横坐标为$2-1=1$或$2+1=3$时,纵坐标的值不小于$1.8+0.5=2.3$,
$\therefore -\frac {1}{4}×3^{2}+3+0.5+h≥2.3$,解得$h≥1.05$,
∴水管高度至少向上调节1.05米,
$1.05+0.5=1.55$(米),
∴水管露出湖面的高度至少调节到约1.55米才能符合要求.
变式.如图1所示的某种发石车是古代一种远程攻击的武器.将发石车置于山坡底部O处,以点O为原点,水平方向为x轴方向,建立如图2所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线$y = a(x - 20)^2 + k$的一部分,山坡OA上有一堵防御墙,其竖直截面为ABCD,墙宽BC = 2米,BC与x轴平行,点B与点O的水平距离为28米,垂直距离为6米.
(1)若发射石块在空中飞行的最大高度为10米.
①求抛物线的解析式;
(2)若要使石块恰好落在防御墙顶部BC上(包括端点B,C),求a的取值范围.
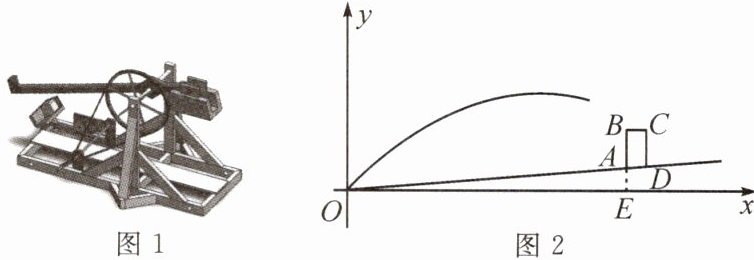
(1)若发射石块在空中飞行的最大高度为10米.
①求抛物线的解析式;
$y=-\frac {1}{40}x^{2}+x$
②试通过计算说明石块能否飞越防御墙?能
(2)若要使石块恰好落在防御墙顶部BC上(包括端点B,C),求a的取值范围.
$-\frac {1}{50}≤a≤-\frac {1}{56}$

答案:
变式.解:
(1)①$y=-\frac {1}{40}x^{2}+x$;
②$B(28,6)$.
当$x=28$时,$y=-\frac {1}{40}×28^{2}+28=8.4>6$;
当$x=30$时,$y=-\frac {1}{40}×30^{2}+30=7.5>6$,
∴石块能飞越防御墙;
(2)$y=a(x-20)^{2}+k$,
过$(0,0),k=-400a,\therefore y=a(x-20)^{2}-400a$,
过B点时,$a=-\frac {1}{56}$;过C点时,$a=-\frac {1}{50}$.
$\therefore -\frac {1}{50}≤a≤-\frac {1}{56}$.
(1)①$y=-\frac {1}{40}x^{2}+x$;
②$B(28,6)$.
当$x=28$时,$y=-\frac {1}{40}×28^{2}+28=8.4>6$;
当$x=30$时,$y=-\frac {1}{40}×30^{2}+30=7.5>6$,
∴石块能飞越防御墙;
(2)$y=a(x-20)^{2}+k$,
过$(0,0),k=-400a,\therefore y=a(x-20)^{2}-400a$,
过B点时,$a=-\frac {1}{56}$;过C点时,$a=-\frac {1}{50}$.
$\therefore -\frac {1}{50}≤a≤-\frac {1}{56}$.
查看更多完整答案,请扫码查看


