《2025年思维新观察九年级数学上册人教版》

1.(2024·武汉)如图,将△ABC绕点C顺时针旋转得到△DEC,点D落在线段AB上.求证:DC平分∠ADE.
证明: ∵AC=CD，∴∠A=∠ADC，又∵∠A=∠CDE，∴∠ADC=∠CDE。

答案： 证明: $\because AC = CD$，$\therefore \angle A = \angle ADC$，又 $\because \angle A = \angle CDE$，$\therefore \angle ADC = \angle CDE$。

2.(2025·武汉)如图,在△ABC中,AC= BC,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BD,BE.
(1)判断△ABD的形状;等边三角形
(2)求证:BE平分∠ABD.
证明: 证△BAE≌△BDE，∴BE平分∠ABD。

答案：
(1) 解: 等边三角形;
(2) 证明: 证 $\triangle BAE \cong \triangle BDE$，$\therefore BE$ 平分 $\angle ABD$。

3.如图,将△ABC绕点A逆时针旋转60°得到△ADE,连接CD,若∠CDE= 78°,求∠BCD的度数.

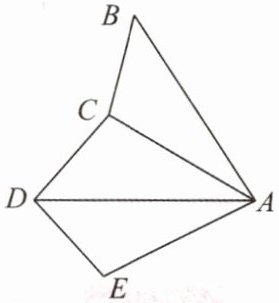
解: 138°。

答案： 解: $138^{\circ}$。

4.(2024·青山)如图,在△ABC中,∠ACB= 120°,将△ABC绕点A顺时针旋转得到△ADE,点C的对应点E恰好落在BC边的延长线上,求证:DE//AC.
证明: 由旋转知AC = AE，∠CAE = ∠BAC，∵点E在BC的延长线上，∠ACB=120°，∴∠ACE = 60°，∴△ACE为等边三角形，∴∠CAE = 60°，∠EAC = 60°（注：此处原答案∠ACE=60°已用，根据逻辑补充∠CAE=60°或∠AEC=60°更合理，若严格按原答案字面顺序则为∠ACE=60°）。又∵∠AED = ∠ACB = 120°，∴∠DEC = ∠AED - ∠AEC = 120° - 60° = 60°，∴∠DEC = ∠ACE，∴DE // AC.

答案： 证明: 由旋转知 $AC = AE$，$\angle ACE = 60^{\circ}$，$\therefore \triangle ACE$ 为等边三角形。又 $\because \angle AED = \angle ACB = 120^{\circ}$，$\therefore \angle DEC = 60^{\circ}$，$\therefore DE // AC$。

5.(2025·武汉)如图,△ABD,△AEC都是等边三角形,△ACD可以由△AEB通过旋转变换得到.
(1)请写出旋转中心、旋转方向及旋转角的大小;
旋转中心:点A，旋转方向:顺时针，旋转角的大小:60°;
(2)BE与CD相交于点O,求∠DOE的度数.
∠DOE的度数为120°.

答案： 解:
(1) 旋转中心: 点 $A$，旋转方向: 顺时针，旋转角 $60^{\circ}$;
(2) $120^{\circ}$。

6.(2020·江岸)如图,P是正三角形ABC外一点,∠APB= 30°,则$PA^2+PB^2= PC^2.$小明为了证明这个结论,将△PBC绕点B逆时针旋转60°,请帮助小明完成他的作图.

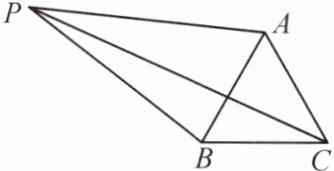
答案：
如图所示。
参考答案 - 17