《2025年思维新观察九年级数学上册人教版》

9.在 $\triangle ABC$ 中,$AB = AC = 5$,$BC = 6$,点 $D$ 是 $BC$ 的中点,以 $D$ 为圆心,2.5 为半径作圆,则 $\odot D$ 与直线 $AC$ 的位置关系是相交.

答案： 相交

10.若 $\odot O$ 的半径为 6,如果一条直线和圆相切,$P$ 为直线上一点,则 $OP$ 的长度的取值范围是(C)
A.$OP = 6$
B.$OP ＞ 6$
C.$OP \geq 6$
D.$OP ＜ 6$

答案： C

11.已知 $\angle MAN = 30^{\circ}$,$O$ 为边 $AN$ 上一点,以 $O$ 为圆心,2 为半径作 $\odot O$,交 $AN$ 于 $D$,$E$ 两点,设 $AD = x$.
(1)如图 1,当 $x$ 取何值时,$\odot O$ 与 $AM$ 相切?2
(2)如图 2,当 $x$ 取何值时,$\odot O$ 与 $AM$ 相交于 $B$,$C$ 两点,且 $\angle BOC = 90^{\circ}$?$2\sqrt{2}-2$

答案： 解:
(1)$x=2$.
(2)$x=2\sqrt {2}-2$,作$OG⊥BC$于G,
则$OG=\sqrt {2},\because ∠A=30^{\circ },$
学参考答案- 22
$\therefore OA=2OG=2\sqrt {2},$
$AD=2\sqrt {2}-2.$

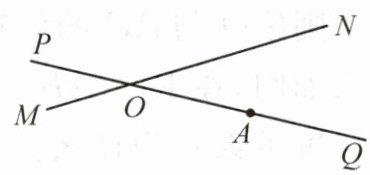
12.(教材 P91T16 变式)如图,铁路 $MN$ 和公路 $PQ$ 在点 $O$ 处交汇,$\angle QON = 30^{\circ}$,在点 $A$ 处有一栋居民楼,$AO = 240$ m,如果火车行驶时周围 200 m 以内会受到噪音的影响,当火车以 72 km/h 的速度行驶时,居民楼受噪音影响的时间为16秒?

答案： 解:以A为圆心,200为半径作$\odot A$交MN于E,F两点,则EF的长为受影响距离,
作$AH⊥MN$于H,连接AF,$\because AO=240,∠QON=30^{\circ },$
$\therefore AH=120,$
在$Rt△AHF$中,
$AF=240,AH=120,$
$\therefore FH=160,$
$EF=320,$
$\therefore t=320÷20=16s.$

13.(2025·汉川)如图,将 $Rt\triangle ABC$ 的顶点 $C$ 放在 $\odot O$ 上,边 $AC$ 与 $\odot O$ 交于点 $D$.已知 $\angle BCA = 60^{\circ}$,$\angle B = 90^{\circ}$,$BC = 6$,$\odot O$ 的半径为 4.当 $AC$ 恰好经过圆心 $O$ 时,求证:$AB$ 是 $\odot O$ 的切线.

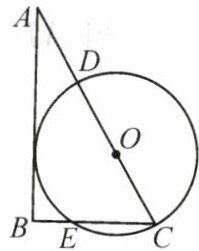
答案： 证明:过点O作$OM⊥AB$于点M,过点O作$ON⊥BC$于点N,
$\therefore ON=BM=2\sqrt {3}$,而$AB=6\sqrt {3},$
$\therefore AM=4\sqrt {3},$
在$Rt△AOM$中,
$OM=\sqrt {8^{2}-(4\sqrt {3})^{2}}=4,$
$\therefore OM=R,\therefore AB$为$\odot O$的切线.