《2025年思维新观察九年级数学上册人教版》

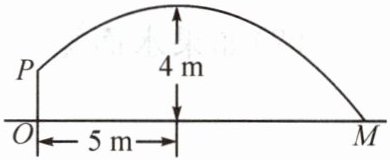
【典例1】(2025·荆门)如图,壮壮同学投掷实心球,出手(点P处)的高度OP是$\frac {7}{4}m$,出手后实心球沿一段抛物线运行,到达最高点时,水平距离是5m,高度是4m.若实心球落地点为M,则$OM= $$\frac{35}{3}$m.

答案： $\frac{35}{3}$
解：设抛物线解析式为：$y = a(x - 5)^2 + 4$，
把点$(0,\frac{7}{4})$代入得$25a + 4 = \frac{7}{4}$，
$\therefore a = -\frac{9}{100}$，$\therefore y = -\frac{9}{100}(x - 5)^2 + 4$，
当$y = 0$时，$-\frac{9}{100}(x - 5)^2 + 4 = 0$，
解得$x_1 = -\frac{5}{3}$（舍去），$x_2 = \frac{35}{3}$，
即此次实心球被推出的水平距离$OM$为$\frac{35}{3}$。

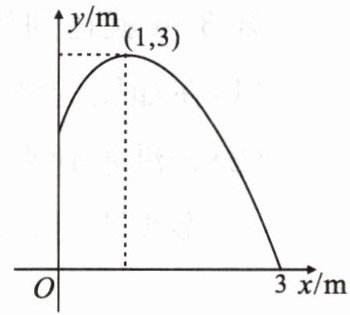
【典例2】(教材P36例4)如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?

解：设抛物线的解析式为$y=a(x-1)^2+3(a\neq0)$，将点$(3,0)$代入得$a=$$-\frac{3}{4}$，$\therefore$抛物线的解析式为$y=$$-\frac{3}{4}(x-1)^2+3$，令$x=0$，得$y=$$\frac{9}{4}$，$\therefore$水管长应为$\frac{9}{4}$m。

答案： 解：$y = a(x - 1)^2 + 3(a \neq 0)$，将$(3,0)$
代入得$a = -\frac{3}{4}$，
$\therefore y = -\frac{3}{4}(x - 1)^2 + 3$，
令$x = 0$，$y = \frac{9}{4}$，
$\therefore$水管长应为$\frac{9}{4}m$。

变式1.(2024·宜昌)如图1,儿童公园草坪的地面O处有一根直立水管,喷水口可上下移动,喷出的抛物线形水线也随之上下平移,图2是其示意图.开始喷水后,若喷水口在O处,水线落地点为A,$OA= 4m$;若喷水口上升1.5m到P处,水线落地点为B,$OB= 6m$.
(1)求水线最高点与点B之间的水平距离;4m
(2)当喷水口在P处时,
①求水线的最大高度;2m
②身高1.68m的小安要从水线下某点经过,为了不被水喷到,该点与O的水平距离应满足什么条件?请说明理由.0.4＜x＜3.6

答案： 解：以$OB$所在的直线为$x$轴，$OP$所在的直线为$y$轴建立平面直角坐标系。
(1)$\because OA = 4$，$\therefore$点$O$坐标为$(0,0)$，点$A$坐标为$(4,0)$，
$\therefore$所得抛物线的对称轴为：直线$x = 2$。
$\because OB = 6$，$\therefore$点$B$的坐标为$(6,0)$，
$\therefore$水线最高点与点$B$之间的水平距离为$6 - 2 = 4(m)$；
(2)①设喷水口在$P$处时，喷出的抛物线形水线的解析式为$y = ax^2 + bx + c(a \neq 0)$。
$\because$经过点$P(0,1.5)$，$B(6,0)$，对称轴与过点$O$的抛物线的对称轴相同，
$\therefore \begin{cases}c = 1.5\\-\frac{b}{2a} = 2\\36a + 6b + c = 0\end{cases}$，解得$\begin{cases}a = -\frac{1}{8}\\b = \frac{1}{2}\\c = \frac{3}{2}\end{cases}$，
$\therefore y = -\frac{1}{8}x^2 + \frac{1}{2}x + \frac{3}{2}$，$\therefore$当$x = 2$时，$y = 2$。
答：水线的最大高度为$2m$；
②当$y = 1.68$时，$1.68 = -\frac{1}{8}x^2 + \frac{1}{2}x + \frac{3}{2}$，
$\therefore x_1 = 0.4$，$x_2 = 3.6$，
$\therefore$为了不被水喷到，该点与$O$的水平距离应满足$0.4 ＜ x ＜ 3.6$。