第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
【典例】【证明体验】如图 1,向$\triangle ABC外作等边\triangle ABD和等边\triangle ACE$,连接$BE$,$DC$。求证:$BE = DC$。
答案:
解:
(1)证明略;
(1)证明略;
【思考探究】如图 2,已知$\triangle ABC$,以$BC为边作等边\triangle BCD$,连接$AD$,若$\angle CAD = 60^{\circ}$,$AD = 4$,$AC = 3$,求$AB$的长。
$AB$的长为
$AB$的长为
$\sqrt{37}$
。
答案:
以AD为边向外作等边△ADE,连接CE,作EF⊥AC,由
(1)知AB=CE=$\sqrt{37}$;
(1)知AB=CE=$\sqrt{37}$;
【拓展延伸】如图 3,在$\triangle ABC$中,$BC = 8$,以$AB为边作等腰\triangle ABD$,$AB = AD$,连接$CD$。若$CD = 10$,$\angle DAB = 2\angle ACB$,直接写出$\triangle ABC$的面积。


12
答案:
作等腰△ACM使AC=AM,∠CAM=∠BAD,连接BM,
∴BM=CD,CM⊥BC,
∴CM=6.作AH⊥CM于H点,
∴CH=3,
∴$S_{\triangle ABC}=\frac{1}{2}\times8\times3=12$.
∴BM=CD,CM⊥BC,
∴CM=6.作AH⊥CM于H点,
∴CH=3,
∴$S_{\triangle ABC}=\frac{1}{2}\times8\times3=12$.
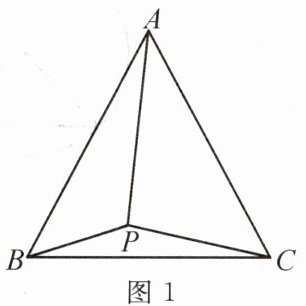
变式.(2023·江汉改编)如图 1,$P为等边\triangle ABC$内一点,$\angle BPC = 150^{\circ}$,连接$AP$。
(1)【作图体验】将$\triangle BPC绕B点逆时针旋转60^{\circ}$,画图;
(2)【模型运用】若$BP = 6$,$CP = 8$,求$AP$的长;
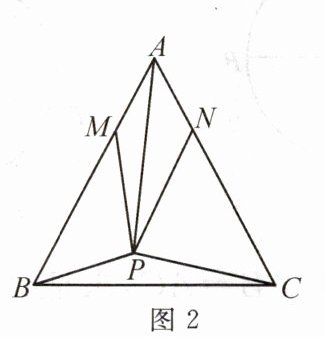
(3)【模型拓展】如图 2,$M$,$N为边AB$,$AC$上动点,且$AM = AN$,在(2)的条件下,求$PM + PN$的最小值;
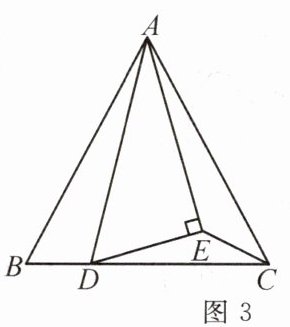
(4)(2024·新洲)如图 3,$D点在等边\triangle ABC的边BC$上,$\angle ADE = 60^{\circ}$,$AE \perp DE$,$CE平分\angle ACD$,求$\frac{BD}{CD}$的值。
(1)【作图体验】将$\triangle BPC绕B点逆时针旋转60^{\circ}$,画图;
(2)【模型运用】若$BP = 6$,$CP = 8$,求$AP$的长;
(3)【模型拓展】如图 2,$M$,$N为边AB$,$AC$上动点,且$AM = AN$,在(2)的条件下,求$PM + PN$的最小值;
(4)(2024·新洲)如图 3,$D点在等边\triangle ABC的边BC$上,$\angle ADE = 60^{\circ}$,$AE \perp DE$,$CE平分\angle ACD$,求$\frac{BD}{CD}$的值。



答案:
解:
(1)如图所示;


(2)由
(1)知△BCP≌△BAE,连接PE,
∴∠AEB=∠BPC=150°,
∴∠AEP=90°.在Rt△APE中,$AP^{2}=PE^{2}+AE^{2}$,
∴$AP=\sqrt{6^{2}+8^{2}}=10$;
(3)以AP为边作等边△APH,连接HN,△APM≌△AHN,
∴NH=PM.在△PNH中,PN+NH>PH,
当P,N,H三点共线时,PN+PM最小为10;

(4)延长DE至F使DE=EF,连接AF,CF,△ABD ≌△ACF,
∴CF=BD,∠ACF=∠B=60°,
∴CE⊥CF.延长DC至G使CG=CD,连接FG,
∴CE//FG.又∠G=30°,
∴$CF=\frac{1}{2}CG$,
∴$\frac{BD}{CD}=\frac{1}{2}$.
解:
(1)如图所示;


(2)由
(1)知△BCP≌△BAE,连接PE,
∴∠AEB=∠BPC=150°,
∴∠AEP=90°.在Rt△APE中,$AP^{2}=PE^{2}+AE^{2}$,
∴$AP=\sqrt{6^{2}+8^{2}}=10$;
(3)以AP为边作等边△APH,连接HN,△APM≌△AHN,
∴NH=PM.在△PNH中,PN+NH>PH,
当P,N,H三点共线时,PN+PM最小为10;

(4)延长DE至F使DE=EF,连接AF,CF,△ABD ≌△ACF,
∴CF=BD,∠ACF=∠B=60°,
∴CE⊥CF.延长DC至G使CG=CD,连接FG,
∴CE//FG.又∠G=30°,
∴$CF=\frac{1}{2}CG$,
∴$\frac{BD}{CD}=\frac{1}{2}$.
查看更多完整答案,请扫码查看


