《2025年思维新观察九年级数学上册人教版》

【典例】如图,AB为$\odot O$的直径,点C和P在$\widehat {AB}$上,AP平分$∠BAC,AB= 10,AC= 6,PM⊥$AB于M,求PM的长.

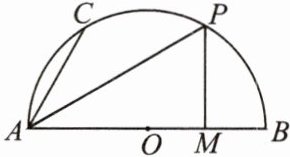
解:连接 OP,作 ON⊥AC 于 N,易证△AON≌△OPM,∴PM=ON=4.

答案： 解:连接 OP,作 ON⊥AC 于 N,易证△AON≌△OPM,
∴PM=ON=4.

变式1.如图,AB是$\odot O$的直径,C,P是$\widehat {AB}$上两点,$AB= 13,AC= 5$,点P是$\widehat {BC}$的中点,求PA的长.

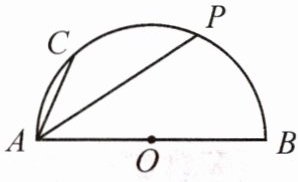
解:连接 BC,OP,PB,设 BC 交 OP 于 E,OE=$\frac{1}{2}$AC=$\frac{5}{2}$.∴PE=4,BE=CE=6,∴PB²=PE²+BE²=52,∴PA²=AB²-PB²=117,∴PA=3$\sqrt{13}$.

答案： 解:连接 BC,OP,PB,设 BC 交 OP 于 E,OE=$\frac{1}{2}$AC=$\frac{5}{2}$.
∴PE=4,BE=CE=6,
∴PB²=PE²+BE²=52,
∴PA²=AB²-PB²=117,
∴PA=3$\sqrt{13}$.

变式2.(2020武汉中考改)如图,若AB为$\odot O$的直径,AC为弦,AP平分$∠BAC交\odot O$于P,交BC于E,$BC= 4\sqrt {2}$,且$AE= PE$,连接PC,PB,求AP的长.

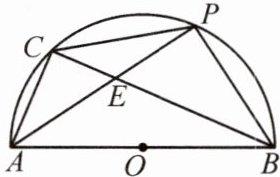
AP的长为$2\sqrt{6}$.

答案： 解:连接 PO 交 BC 于 M,易证△ACE≌△PME,PM=AC,设 OM=x,则 AC=PM=2x,在 Rt△BOM 中,x²+(2$\sqrt{2}$)²=(3x)²,x=1(x=-1 已舍),AB=6,BP=2$\sqrt{3}$,
∴AP=$\sqrt{36 - 12}$=2$\sqrt{6}$.