《2025年综合应用创新题典中点八年级数学上册北师大版》

4. 立德树人 爱国主义 某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图①)到爱国主义教育基地进行研学.上午8:00,军车在离营地60km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地,军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图②所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值；函数表达式为s = 20 + 40t，a的值为2
(2)求部队官兵在仓库领取物资所用的时间.所用时间为$\frac{1}{3}$h

答案： 【解】
(1)大巴的速度为 $ \frac{60 - 20}{1} = 40 $ (km/h)，所以大巴离营地的路程 $ s $ 与所用时间 $ t $ 的函数表达式为 $ s = 20 + 40t $. 当 $ s = 100 $ 时，$ 100 = 20 + 40a $，解得 $ a = 2 $.
(2)由题图②可得，军车速度为 $ 60 \div 1 = 60 $ (km/h)，设部队官兵在仓库领取物资所用的时间为 $ x $ h，根据题意，得 $ 60(2 - x) = 100 $，解得 $ x = \frac{1}{3} $. 所以部队官兵在仓库领取物资所用的时间为 $ \frac{1}{3} $ h.

5. 目前,某市对市区居民用气户的燃气收费,以户为基础、年为计算周期设定了如下表的三个气量阶梯：

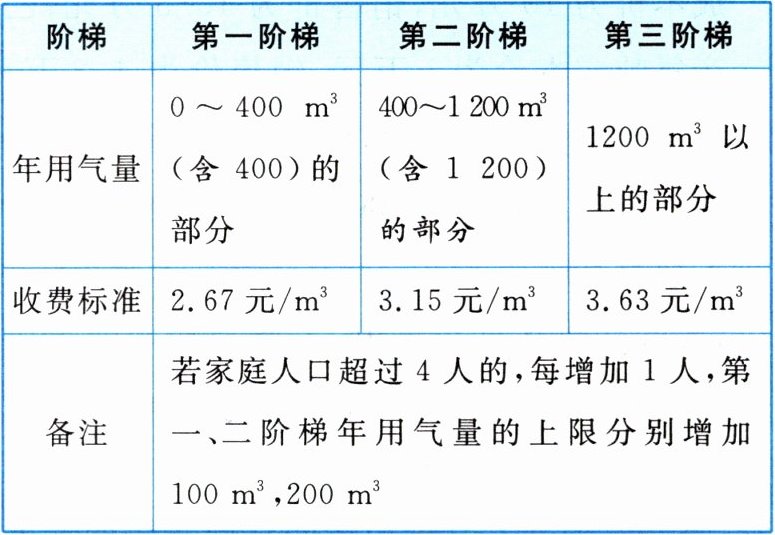
(1)一户家庭人口为3人,年用气量为$200m^{3}$,则该年此户需缴纳燃气费用为____534元；
(2)一户家庭人口不超过4人,年用气量为$xm^{3}(x＞1200)$,该年此户需缴纳燃气费用为y元,求y与x的函数表达式；
(3)甲户家庭人口为3人,乙户家庭人口为5人,某年甲户、乙户缴纳的燃气费用均为3855元,求该年乙户比甲户多用多少立方米的燃气.(结果精确到$1m^{3}$)

答案： 【解】
(1)534
(2)根据题意，得 $ y = 400 \times 2.67 + (1200 - 400) \times 3.15 + 3.63(x - 1200) = 3.63x - 768 $，所以 $ y $ 与 $ x $ 的函数表达式为 $ y = 3.63x - 768(x ＞ 1200) $.
(3)因为 $ 400 \times 2.67 + (1200 - 400) \times 3.15 = 3588 $ (元) $ ＜ 3855 $ 元，所以甲户该年的用气量达到了第三阶梯. 由
(2)知，当 $ y = 3855 $ 时，$ 3.63x - 768 = 3855 $，解得 $ x \approx 1273.6 $. 又因为 $ 2.67 \times (100 + 400) + 3.75 \times [1200 + 200 - (100 + 400)] = 4170 $ (元) $ ＞ 3855 $ 元，且 $ 2.67 \times (100 + 400) = 1335 $ (元) $ ＜ 3855 $ 元，所以乙户该年的用气量达到第二阶梯，但未达到第三阶梯. 设乙户年用气量为 $ a $ $ m^3 $，则有 $ 2.67 \times (100 + 400) + 3.15[a - (100 + 400)] = 3855 $，解得 $ a = 1300 $，$ 1300 - 1273.6 \approx 26 $ ($ m^3 $). 答：该年乙户比甲户多用约 $ 26 $ $ m^3 $ 的燃气.