第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 四根小棒的长分别是5,9,12,13,从中选择三根小棒首尾相接,搭成边长如下的四个三角形,其中是直角三角形的是 (
A. 5,9,12
B. 5,9,13
C. 5,12,13
D. 9,12,13
C
)A. 5,9,12
B. 5,9,13
C. 5,12,13
D. 9,12,13
答案:
C
2. 在$\triangle ABC$中,$∠A,∠B,∠C$所对的边分别为a,b,c,下列条件中,不能判定$\triangle ABC$为直角三角形的是 (
A. $a:b:c= 5:12:13$
B. $∠A:∠B:∠C= 2:3:5$
C. $a= 9k,b= 40k,c= 41k(k>0)$
D. $a= 3^{2},b= 4^{2},c= 5^{2}$
D
)A. $a:b:c= 5:12:13$
B. $∠A:∠B:∠C= 2:3:5$
C. $a= 9k,b= 40k,c= 41k(k>0)$
D. $a= 3^{2},b= 4^{2},c= 5^{2}$
答案:
D
3. 若三角形的三边长分别为a,b,c,且满足$(a+b)^{2}-c^{2}= 2ab$,则此三角形中最大的角是(
A. 锐角
B. 直角
C. 钝角
D. 无法确定
B
)A. 锐角
B. 直角
C. 钝角
D. 无法确定
答案:
B
4. 如图,在由小正方形组成的$3×2$网格中,每个小正方形的顶点称为格点.点A,B,C,D,M,N均在格点上,其中点A,B,C,D能与点M,N构成一个直角三角形的是 (
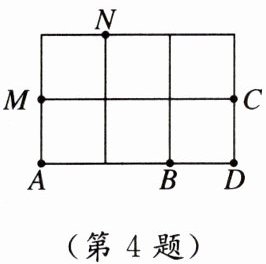
A. 点A
B. 点B
C. 点C
D. 点D
D
)
A. 点A
B. 点B
C. 点C
D. 点D
答案:
D
5. 新考法 逆向思维法 已知$\triangle ABC$中,$AB= k,AC= k+1,BC= 3$,当$k= $
4
时,$∠B= 90^{\circ }$.
答案:
4
6. 如图,$\triangle ABC$中,$AC= 5,BC= 12,AB= 13$,P为直线AB上一动点,连接PC,则线段PC的最小值是
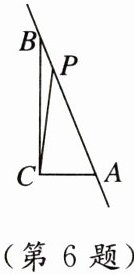
$\frac{60}{13}$
.
答案:
$\frac{60}{13}$
7. [2025徐州期中] 如图,把一块$\triangle ABC土地划出一个\triangle ACD$后,测得$CD= 3$米,$AD= 4$米,$BC= 12$米,$AB= 13$米,其中$∠ACB= 90^{\circ }$.
(1)判断$\triangle ACD$的形状,并说明理由;
$\triangle ACD$是
理由:因为∠ACB=90°,BC=12米,AB=13米,
所以由勾股定理得AC=
(2)求图中阴影部分土地的面积.
图中阴影部分土地的面积=
(1)判断$\triangle ACD$的形状,并说明理由;
$\triangle ACD$是
直角三角形
.理由:因为∠ACB=90°,BC=12米,AB=13米,
所以由勾股定理得AC=
5
米.又因为CD=3米,AD=4米,所以AD²+CD²=25=AC²,所以△ACD是直角三角形,∠ADC=90°.(2)求图中阴影部分土地的面积.
图中阴影部分土地的面积=
24
平方米.
答案:
(1)△ACD是直角三角形.
理由:因为∠ACB=90°,BC=12米,AB=13米,
所以由勾股定理得AC=5米.又因为CD=3米,AD=4米,所以AD²+CD²=25=AC²,所以△ACD是直角三角形,∠ADC=90°.
(2)图中阴影部分土地的面积=$\frac{1}{2}$AC×BC−$\frac{1}{2}$AD×CD=$\frac{1}{2}$×5×12−$\frac{1}{2}$×4×3=24(平方米).
点方法:将求四边形面积的问题可转化为求两个直角三角形面积和或差的问题,解题时要利用题目信息构造出直角三角形,如角度,三边长度等.
(1)△ACD是直角三角形.
理由:因为∠ACB=90°,BC=12米,AB=13米,
所以由勾股定理得AC=5米.又因为CD=3米,AD=4米,所以AD²+CD²=25=AC²,所以△ACD是直角三角形,∠ADC=90°.
(2)图中阴影部分土地的面积=$\frac{1}{2}$AC×BC−$\frac{1}{2}$AD×CD=$\frac{1}{2}$×5×12−$\frac{1}{2}$×4×3=24(平方米).
点方法:将求四边形面积的问题可转化为求两个直角三角形面积和或差的问题,解题时要利用题目信息构造出直角三角形,如角度,三边长度等.
8. 如图,有四个三角形,各有一边长为6,一边长为8,若第三边的长分别为6,8,10,12,则面积最大的三角形是 (
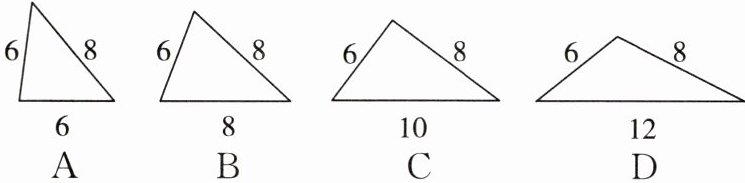
C
)
答案:
C
9. 新考法 等线段代换法 如图,在$\triangle ABC$中,$AB= 6$,$AC= 10$,BC边上的中线$AD= 4$,则$\triangle ABC$的面积为 (
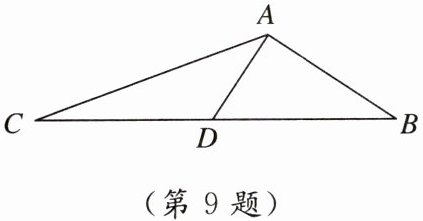
A. 30
B. 24
C. 20
D. 48
B
)
A. 30
B. 24
C. 20
D. 48
答案:
B [点拨]延长AD到E,使DE=AD,连接CE.因为AD为BC边上的中线,所以DC=BD.又因为∠ADB=∠EDC,所以△ADB≌△EDC,所以CE=AB=6,S△ADB=S△EDC,所以S△ABC=S△ACE.又因为AE=2AD=8,AC=10,所以AC²=AE²+CE²,所以△ACE为直角三角形,∠E=90°,所以S△ABC=S△ACE=$\frac{1}{2}$CE·AE=$\frac{1}{2}$×6×8=24.
10. 如图所示的是$3×2$的正方形网格,每个小正方形的顶点称为格点.线段AB,CD的端点均在格点上,且交于点O,则$∠BOD$的度数为 ( )
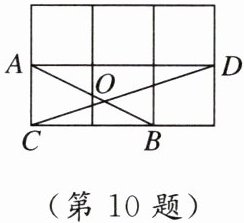
A. $30^{\circ }$
B. $45^{\circ }$
C. $50^{\circ }$
D. $60^{\circ }$

A. $30^{\circ }$
B. $45^{\circ }$
C. $50^{\circ }$
D. $60^{\circ }$
答案:
B [点拨]设小正方形的边长为1.如图,取格点E,连接AE,BE,易知AE//CD,所以∠BAE=∠BOD.由勾股定理得AB²=1²+2²=5,EB²=1²+2²=5,AE²=1²+3²=10,所以AB²+BE²=AE²,AB=BE.所以△ABE是等腰直角三角形.所以∠BAE=45°.所以∠BOD=45°.

B [点拨]设小正方形的边长为1.如图,取格点E,连接AE,BE,易知AE//CD,所以∠BAE=∠BOD.由勾股定理得AB²=1²+2²=5,EB²=1²+2²=5,AE²=1²+3²=10,所以AB²+BE²=AE²,AB=BE.所以△ABE是等腰直角三角形.所以∠BAE=45°.所以∠BOD=45°.

11. 新考向 数学文化 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a,b,c,其中a,b均小于c,$a= \frac {1}{2}m^{2}-\frac {1}{2},c= \frac {1}{2}m^{2}+\frac {1}{2}$,m是大于1的奇数,则$b=$
m
(用含m的式子表示).
答案:
m [点拨]由题意得b²=c²−a²=($\frac{1}{2}$m²+$\frac{1}{2}$)²−($\frac{1}{2}$m²−$\frac{1}{2}$)²=m².因为m是大于1的奇数,所以b=m.
查看更多完整答案,请扫码查看


