《2025年综合应用创新题典中点八年级数学上册北师大版》

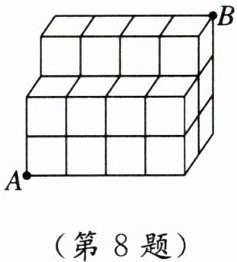
8. [2025青岛期中]如图,由20个棱长为1的小正方体搭成一个组合体,蚂蚁从左下角点A爬到右上角点B的最短路线长的平方是______41.

答案： 41

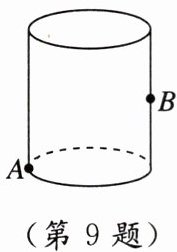
9. 如图,一个圆柱形容器的高为8dm,底面半径为$\frac {9}{π}dm$,在容器内壁中点B处有一只蚊子,此时一只壁虎正好在容器外壁的底部与蚊子相对的点A处,壁虎捕捉蚊子的最短距离为______dm.(容器厚度忽略不计)

答案：
15 【点拨】如图,将圆柱形容器侧面展开,作点B关于直线EF的对称点D,连接AD,易知AD为壁虎捕捉虫子的最短距离.由题意易得,$AC = 2\pi\times\frac{9}{\pi}\times\frac{1}{2}=9(\mathrm{dm})$,$CD = 8+\frac{1}{2}\times8 = 12(\mathrm{dm})$.在$Rt\triangle ACD$中,由勾股定理得$AD^{2}=AC^{2}+DC^{2}=9^{2}+12^{2}=15^{2}$,所以AD = 15dm.即壁虎捕捉蚊子的最短距离为15dm.
　　　　　　　　　　　　　　　　　

10. 新考法 分类讨论法 如图,一圆柱高20cm,底面周长是12cm,一只螳螂在AB的中点E处,一只昆虫在CD的某处,螳螂以最快的速度、最短的爬行距离捕捉到了昆虫,螳螂共爬行了10cm,那么此时昆虫离点C的距离为多少厘米?

答案：
【解】沿AB把圆柱的侧面展开,如图所示.
①设昆虫在CD边上的F处,过F作AB的垂线,垂足为M,连接EF,则EF为最短爬行距离,根据题意知$AC=\frac{1}{2}AA^{\prime}=\frac{1}{2}\times12 = 6(\mathrm{~cm})$,$AE=\frac{1}{2}AB=\frac{1}{2}\times20 = 10(\mathrm{~cm})$.易得MF = AC = 6cm,EF = 10cm,所以由勾股定理得ME = 8cm.
所以易得$FC = MA = EA - EM = 10 - 8 = 2(\mathrm{~cm})$;
②设昆虫在CD边上的$F^{\prime}$处,过$F^{\prime}$作AB的垂线,垂足为N,连接$EF^{\prime}$,则$EF^{\prime}$为最短爬行距离,
同理可得,EN = 8cm,所以易得$F^{\prime}C = NA = NE + EA = 8 + 10 = 18(\mathrm{~cm})$.综上所述,昆虫离点C的距离为2cm或18cm.
　　　　　　　　　　　　　　　　　　　

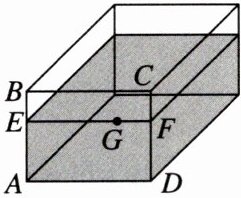
11. 有一个如图所示的长方体透明玻璃水缸,高$AB= 6dm$,水深$AE= 4dm$,在水面线EF上紧贴内壁G处有一粒食物,且$EG= 6dm$,一只小虫想从水缸外的A处沿水缸壁爬到水缸内的G处吃掉食物.
(1)小虫应该沿怎样的路线爬行才能使爬行的路程最短?请你画出最短路线,并用箭头标注.
(2)求小虫爬行的最短路程长(不计缸壁厚度).

答案：
【解】
(1)如图,作点A关于BC所在直线的对称点$A^{\prime}$,连接$A^{\prime} G$,交BC于点Q,连接AQ,则$AQ \to QG$为最短路线.
　　　　　　　　　　　　　　　　　　　
(2)因为AE = 4dm,$AA^{\prime}=2AB = 12 \mathrm{dm}$,所以$A^{\prime} E = 8 \mathrm{dm}$.
在$Rt\triangle A^{\prime} EG$中,EG = 6dm,$A^{\prime} E = 8 \mathrm{dm}$,$A^{\prime} G^{2}=A^{\prime} E^{2}+EG^{2}$,所以$A^{\prime} G = 10 \mathrm{dm}$.
由对称性可知$AQ = A^{\prime} Q$,
所以$AQ + QG = A^{\prime} Q + QG = A^{\prime} G = 10 \mathrm{dm}$.
故小虫爬行的最短路程长为10dm.

12. 如图①,已知圆柱底面的周长为12,圆柱的高为8,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是______.

(2)金属丝的长为______.
(3)如图②,圆柱形玻璃杯的高为9cm,底面周长为16cm,在杯内壁离杯底4cm的点A处有一滴蜂蜜,此时一只蚂蚁正好在外壁上,离杯上沿1cm,且与蜂蜜相对的点B处,则蚂蚁从外壁B处到内壁A处所爬行的最短路程是多少?(杯壁厚度不计)

答案：
【解】
(1)A
(2)20
(3)如图,将玻璃杯侧面展开,作B关于EF的对称点$B^{\prime}$,连接$AB^{\prime}$交EF于点M,易知$AB^{\prime}$为最短路程.作$B^{\prime} D \perp AF$,交AF的延长线于点D.
易得$B^{\prime} D=\frac{1}{2}\times16 = 8(\mathrm{~cm})$,$AD = FA + DF = (9 - 4)+1 = 6(\mathrm{~cm})$.在$Rt\triangle ADB^{\prime}$中,由勾股定理得$AB^{\prime}=10 \mathrm{~cm}$,即蚂蚁从外壁B处到内壁A处所爬行的最短路程为10cm.