《2025年综合应用创新题典中点八年级数学上册北师大版》

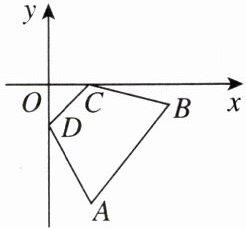
10. 新考法最值探究法 如图,在直角坐标系中,$A(2,-6)$,$B(6,-1)$,$C(m,0)$,$D(0,n)$,当四边形$ABCD$周长最小时,$\frac{m}{n}$的值是______.

答案：
-$\frac{8}{7}$　[点拨]如图，分别作点A(2, -6)关于y轴的对称点为A'(-2, -6)，点B(6, -1)关于x轴的对称点为B'(6, 1)，连接A'B'，交y轴于点D，交x轴于点C，此时四边形ABCD周长最小。设直线A'B'的表达式为y = kx + b，则$\begin{cases}-2k + b = -6 \\ 6k + b = 1 \end{cases}$，解得$\begin{cases}k = \frac{7}{8} \\ b = -\frac{17}{4} \end{cases}$，所以y = $\frac{7}{8}$x - $\frac{17}{4}$。当y = 0时，$\frac{7}{8}$x - $\frac{17}{4}$ = 0，解得x = $\frac{34}{7}$；当x = 0时，y = -$\frac{17}{4}$，所以C($\frac{34}{7}$, 0)，D(0, -$\frac{17}{4}$)。所以m = $\frac{34}{7}$，n = -$\frac{17}{4}$。所以$\frac{m}{n}$ = -$\frac{8}{7}$。

11. 在一条笔直的道路上依次有$A$,$B$,$C$三地,快快同学从$A地跑步到C$地,同时乐乐同学从$B地跑步到A$地,休息1min后接到通知,要求乐乐比快快早1min到达$C$地,两人均匀速运动,如图所示为两人距$A地路程s(\text{m})与快快跑步时间t(\text{min})$之间的函数图象.
(1)$a= $2,乐乐去$A$地的速度为200$\text{m}/\text{min}$；
(2)结合图象,求出乐乐从$A地到C$地对应的函数表达式(写出自变量的取值范围)；
(3)请直接写出两人与$B$地的距离相等的时间.$\frac{8}{7}\min$或$\frac{34}{9}\min$或6min或8min

答案： [解]
(1)2；200
(2)设乐乐从A地到C地对应的函数表达式为s = kt + b (k ≠ 0)。因为F(3, 0)，G(7, 1200)在该函数图象上，所以$\begin{cases}3k + b = 0 \\ 7k + b = 1200 \end{cases}$，解得$\begin{cases}k = 300 \\ b = -900 \end{cases}$。所以乐乐从A地到C地对应的函数表达式为s = 300t - 900(3 ≤ t ≤ 7)。
(3)$\frac{8}{7}$min或$\frac{34}{9}$min或6min或8min　[点拨]设线段OH对应的函数表达式为s = mt(k ≠ 0)。因为H(8, 1200)在函数图象上，所以8m = 1200，解得m = 150。所以线段OH对应的函数表达式为s = 150t(0 ≤ t ≤ 8)。①当0 ≤ t ≤ 2时，200t = 400 - 150t，解得t = $\frac{8}{7}$；②当2 ≤ t ≤ 3时，400 = 150t - 400，解得t = $\frac{16}{3}$(不合题意，舍去)；③当3 ≤ t ≤ 7时，400 - (300t - 900) = 150t - 400或300t - 900 = 150t，解得t = $\frac{34}{9}$或t = 6；④当t = 8时，两人距B地的路程相等。综上所述，两人与B地的距离相等的时间为$\frac{8}{7}$min或$\frac{34}{9}$min或6min或8min。

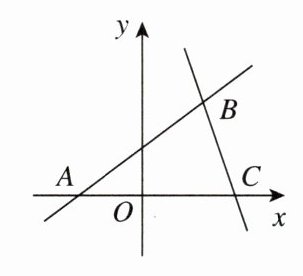
12. [2025眉山期末]如图,在平面直角坐标系中,直线$l:y= \frac{3}{4}x+\frac{3}{2}与x轴交于点A且经过点B(2,m)$,直线$BC与x轴交于点C(3,0)$.
(1)求直线$BC$的函数表达式；
(2)在线段$BC上找一点D$,使得$\triangle ABO与\triangle ABD$的面积相等,求出点$D$的坐标；
(3)$y轴上有一动点P$,直线$BC上有一动点M$,若$\triangle APM是以线段AM$为斜边的等腰直角三角形,请直接写出点$M$的坐标.

答案：
[解]
(1)因为直线l: y = $\frac{3}{4}$x + $\frac{3}{2}$经过点B(2, m)，所以m = $\frac{3}{4}$×2 + $\frac{3}{2}$ = 3。所以B(2, 3)。设直线BC的函数表达式为y = kx + b，将B(2, 3)，C(3, 0)的坐标代入，得$\begin{cases}2k + b = 3 \\ 3k + b = 0 \end{cases}$，解得$\begin{cases}k = -3 \\ b = 9 \end{cases}$，所以直线BC的函数表达式为y = -3x + 9。
(2)如图①，过点O作OD//AB交BC于D，由平行线间距离相等可知，△ABO与△ABD的面积相等。

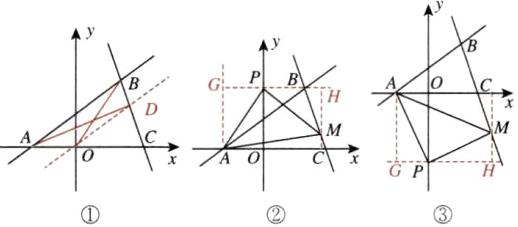
因为直线AB的表达式为y = $\frac{3}{4}$x + $\frac{3}{2}$，所以直线OD的表达式为y = $\frac{3}{4}$x。联立，得$\begin{cases}y = \frac{3}{4}x \\ y = -3x + 9 \end{cases}$，解得$\begin{cases}x = \frac{12}{5} \\ y = \frac{9}{5} \end{cases}$，所以D($\frac{12}{5}$, $\frac{9}{5}$)。
(3)点M的坐标为($\frac{11}{4}$, $\frac{3}{4}$)或($\frac{7}{2}$, -$\frac{3}{2}$)。　[点拨]易得A(-2, 0)，所以OA = 2。①当点P在AM上方时，过点P作x轴的平行线分别与过A，M的y轴平行线交于点G，H，如图②，则GP = OA = 2。设点P的坐标为(0, n)，点M的坐标为(m, 9 - 3m)。因为∠GPA + ∠GAP = 90°，∠GPA + ∠HPM = 90°，所以∠GAP = ∠HPM。又因为PA = PM，∠AGP = ∠PHM = 90°，所以△AGP≌△PHM(AAS)。所以GP = HM = 2，GA = PH。所以$\begin{cases}n - (9 - 3m) = 2 \\ m = n \end{cases}$，解得$\begin{cases}m = \frac{11}{4} \\ n = \frac{11}{4} \end{cases}$，所以点M的坐标为($\frac{11}{4}$, $\frac{3}{4}$)；②当点P在AM下方时，过点P作x轴的平行线分别与过A，M的y轴平行线交于点G，H，如图③，则GP = OA = 2。设点P的坐标为(0, n)，点M的坐标为(m, 9 - 3m)。因为∠GPA + ∠GAP = 90°，∠GPA + ∠HPM = 90°，所以∠GAP = ∠HPM。又因为PA = PM，∠AGP = ∠PHM = 90°，所以△AGP≌△PHM(AAS)。所以GP = HM = 2，GA = PH。所以$\begin{cases}9 - 3m - n = 2 \\ m = -n \end{cases}$，解得$\begin{cases}m = \frac{7}{2} \\ n = -\frac{7}{2} \end{cases}$，所以点M的坐标为($\frac{7}{2}$, -$\frac{3}{2}$)。综上，点M的坐标为($\frac{11}{4}$, $\frac{3}{4}$)或($\frac{7}{2}$, -$\frac{3}{2}$)。