第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. 真实情境题 航天科技 我国神舟十八号载人飞船在太空飞行了192天,并于2024年11月4日成功着陆,下列描述能确定飞船着陆位置的是(
A. 内蒙古西部
B. 酒泉卫星发射中心东南方向
C. 东经$100^{\circ }03'08''$,北纬$41^{\circ }39'12''$
D. 东经$100^{\circ }03'08''$
C
)A. 内蒙古西部
B. 酒泉卫星发射中心东南方向
C. 东经$100^{\circ }03'08''$,北纬$41^{\circ }39'12''$
D. 东经$100^{\circ }03'08''$
答案:
C
2. 如图,已知$∠AOC= 30^{\circ },∠BOC= 150^{\circ }$,OD平分$∠BOA$,若点A表示为$(2,30^{\circ })$,点B表示为$(4,150^{\circ })$,则点D表示为(
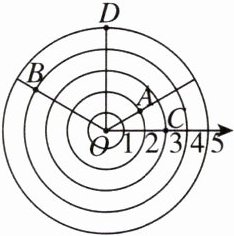
A. $(5,90^{\circ })$
B. $(5,75^{\circ })$
C. $(5,60^{\circ })$
D. $(5,120^{\circ })$
A
)
A. $(5,90^{\circ })$
B. $(5,75^{\circ })$
C. $(5,60^{\circ })$
D. $(5,120^{\circ })$
答案:
A
3. 新趋势 学科内综合 在平面直角坐标系中,若点A的坐标为$(\sqrt {a^{2}+1},b^{2}+3)$,则点A所在的象限是(
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
A
)A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
答案:
A
4. 已知点P在第四象限,且到x轴的距离为2,到y轴的距离为3,则点P的坐标为
(3,-2)
.
答案:
$(3,-2)$
5. 点$P(m+2,m-4)$在x轴上,则点P的坐标为
$(6,0)$
.
答案:
$(6,0)$
6. 情境题 中国象棋 中国象棋文化历史久远,雅俗共赏,具有广泛的参与度.象棋残局是象棋的基础,如图就是某次对弈的残局图.如果建立平面直角坐标系,使“帅”位于点$(-1,-2)$,“象”位于点$(-2,5)$,那么“兵”在同一坐标系下的坐标是(

A. $(1,3)$
B. $(2,3)$
C. $(2,2)$
D. $(3,2)$
C
)
A. $(1,3)$
B. $(2,3)$
C. $(2,2)$
D. $(3,2)$
答案:
C
7. [2025深圳罗湖区月考]已知点$P(a+b,3),Q(2,-b)$关于y轴对称,则ab的值是(
A. -1
B. 2
C. -3
D. 3
C
)A. -1
B. 2
C. -3
D. 3
答案:
C
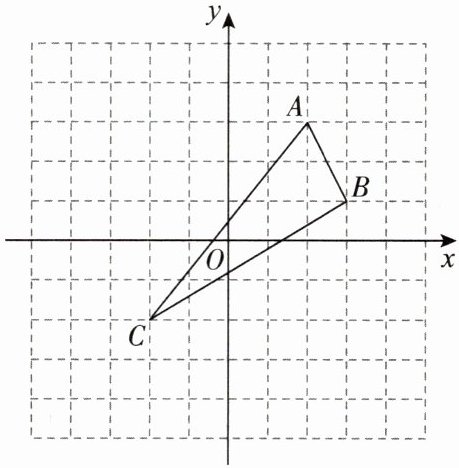
8. 在如图的直角坐标系中,每个小方格都是边长为1个单位的正方形,$\triangle ABC$的三个顶点都在格点上(每个小正方形的顶点叫格点),点A的坐标为$(2,3)$.
(1)请画出$\triangle ABC$关于y轴对称的$\triangle A'B'C'$(其中$A',B',C'$分别是A,B,C的对应点);
(2)写出$A',B',C'$三点的坐标:____.
(3)若在y轴上有一点P,使得$PA+PB$的值最小,请画出点P的位置.
(1)请画出$\triangle ABC$关于y轴对称的$\triangle A'B'C'$(其中$A',B',C'$分别是A,B,C的对应点);
(2)写出$A',B',C'$三点的坐标:____.
(3)若在y轴上有一点P,使得$PA+PB$的值最小,请画出点P的位置.

答案:
【解】
(1)如图所示,$\triangle A'B'C'$ 即为所求.

(2)$A'(-2,3)$,$B'(-3,1)$,$C'(2,-2)$
(3)如图所示,点 $P$ 即为所求.
【解】
(1)如图所示,$\triangle A'B'C'$ 即为所求.

(2)$A'(-2,3)$,$B'(-3,1)$,$C'(2,-2)$
(3)如图所示,点 $P$ 即为所求.
9. [2025成都锦江区期中]如图所示,在平面直角坐标系中,已知$A(1,1),B(3,0),C(2,3)$.
(1)在平面直角坐标系中画出$\triangle ABC$,$\triangle ABC$的面积是____;
(2)若点D与点A关于y轴对称,点E与点B关于y轴对称,点F与点C关于x轴对称,画出$\triangle DFE$,写出点F的坐标为____;
(3)已知P为坐标轴上的一点,若$\triangle ABP$的面积为3,求点P的坐标.
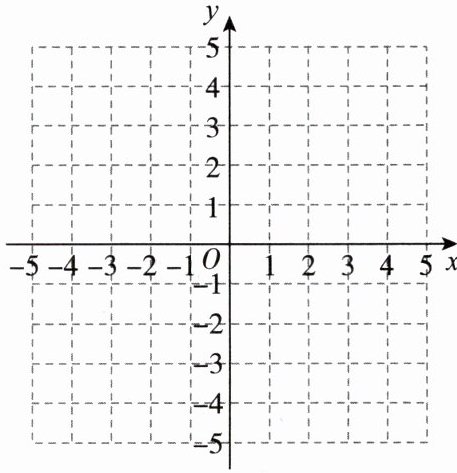
(1)在平面直角坐标系中画出$\triangle ABC$,$\triangle ABC$的面积是____;
(2)若点D与点A关于y轴对称,点E与点B关于y轴对称,点F与点C关于x轴对称,画出$\triangle DFE$,写出点F的坐标为____;
(3)已知P为坐标轴上的一点,若$\triangle ABP$的面积为3,求点P的坐标.

答案:
【解】
(1)如图,$\triangle ABC$ 即为所求.
$\frac{5}{2}$
(2)如图,$\triangle DEF$ 即为所求.

$(2,-3)$
(3)分情况讨论:①当点 $P$ 在 $x$ 轴上时,因为 $\triangle ABP$ 的面积为 $3$,$A(1,1)$,所以 $\frac{1}{2}BP \times 1 = 3$. 所以 $BP = 6$.
所以点 $P$ 的坐标为 $(-3,0)$ 或 $(9,0)$;
②当点 $P$ 在 $y$ 轴上时,因为 $\triangle ABP$ 的面积为 $3$.
设 $P(0,m)$,当 $m$ 在负半轴上时,$3 \times |1 - m| - \frac{1}{2} \times |1 - m| \times 1 - \frac{1}{2} \times |m| \times 3 - \frac{1}{2} \times 2 \times 1 = 3$,整理得 $5|1 - m| - 3|m| = 8$,即 $5 - 5m + 3m = 8$,解得 $m = -\frac{3}{2}$;
当 $m$ 在正半轴上时,$\frac{1}{2} \times m \times 3 - \frac{1}{2}m \times 1 - \frac{1}{2} \times 3 \times 1 = 3$,解得 $m = \frac{9}{2}$.
所以点 $P$ 的坐标为 $(0,-\frac{3}{2})$ 或 $(0,\frac{9}{2})$ 或 $(-3,0)$ 或 $(9,0)$.
【解】
(1)如图,$\triangle ABC$ 即为所求.
$\frac{5}{2}$
(2)如图,$\triangle DEF$ 即为所求.

$(2,-3)$
(3)分情况讨论:①当点 $P$ 在 $x$ 轴上时,因为 $\triangle ABP$ 的面积为 $3$,$A(1,1)$,所以 $\frac{1}{2}BP \times 1 = 3$. 所以 $BP = 6$.
所以点 $P$ 的坐标为 $(-3,0)$ 或 $(9,0)$;
②当点 $P$ 在 $y$ 轴上时,因为 $\triangle ABP$ 的面积为 $3$.
设 $P(0,m)$,当 $m$ 在负半轴上时,$3 \times |1 - m| - \frac{1}{2} \times |1 - m| \times 1 - \frac{1}{2} \times |m| \times 3 - \frac{1}{2} \times 2 \times 1 = 3$,整理得 $5|1 - m| - 3|m| = 8$,即 $5 - 5m + 3m = 8$,解得 $m = -\frac{3}{2}$;
当 $m$ 在正半轴上时,$\frac{1}{2} \times m \times 3 - \frac{1}{2}m \times 1 - \frac{1}{2} \times 3 \times 1 = 3$,解得 $m = \frac{9}{2}$.
所以点 $P$ 的坐标为 $(0,-\frac{3}{2})$ 或 $(0,\frac{9}{2})$ 或 $(-3,0)$ 或 $(9,0)$.
查看更多完整答案,请扫码查看


